�Q�̕���������͂��Ă݂���
�u�Q�̕�������v�Ƃ����Ђ��������ɂ��āA�l�b�g��ł����ȉ���������ă\�[�g�[�ʔ����l�B�}�g�Ă�����̂�����A���Ⴂ���Ă���́A���ɂ͊ԈႢ�X�Ɛ����Ƃ��ďo���Ă�������B���ł���������Ƃ������������Ƃ��Ȃ��Ƃ��E�E�E�B
��{�I�ɂ́A����Ȃ����ɘf�킳��āA���ς��čl���Ă��邤���ɁA�ŏ��̐ݒ肩�炸��܂���Ƃ����p�^�[���B���̉��߂��珑�������Ă��܂�������A���Θ_�̃g���b�N�Ƃ�������B
�������Ⴂ�̌����ŁA�����p���h�N�X�Ɗ����錴���Ȃ̂��A�������肳���Ă�������������悤�Ȃ̂ŁA�ƒf�ƕΌ��ʼn�͂��Ă݂����B
���̌��ʁA
point
�u�Q�̕����̃p���h�N�X�v�́A�m���v�Z�̊��Ⴂ�ŁA
��Ɩ��̐ݒ�������ς��Ă��܂����߂��������Ă���B
�Ƃ������Ƃ��킩�����B
�Ƃ͌������̂́A�l�b�g�ł���Ɠ����咣��������Ȃ������̂ŁA�Ԉ���Ă�\�����E�E�E�B���������Ė{���ɖ������������̂��i�H�@��[���l���ăl�B
�@�Q�̕�������i��{�`�j
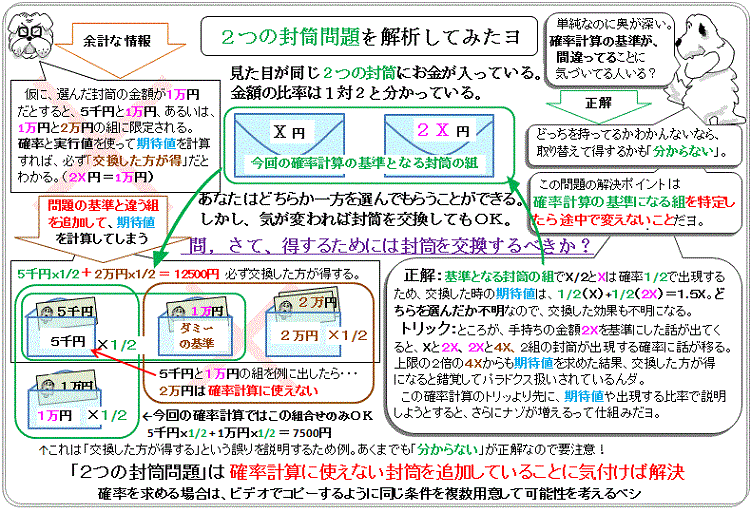
���������Ȃ��Q�̕����ɂ����������Ă�B���z�̊������P���Q�B
���������Ȃ���ԂŁA�I�����̒��̂��������炤���Ƃ��ł���B
������I��ŁA�c�����������������邩�������B
�@�@�@
���@���āA��蓾����ɂ́A��������������ׂ��H
- ���z�����肵����@�Ŗ�蔭���I
�Q�̕������̊�{�`�ł́A�u�킩��Ȃ��v���������B���̌�A�����������@�ɏ]���A�ݒ��ς���̂��p���h�N�X�̉����Ǝv���Ă���B���́A���ꂪ�p���h�N�X�̎n�܂�B
- �u�Q�̕������v�̖ӓ_���m�F���Ă�����
�ݒ��ς��ăp���h�N�X���������O�ɁA�܂��A��肪�ǂ̂悤�ɏ�������Ă��邩��F�����āA���Ⴂ�����Ă��Ȃ����m�F���Ă������B
���P �܂����Ǝv���Ă��u���Ғl�v�Z�v����������
���Q ���������C�x���g�͓����ʼn������ׂ�
���R ���z�̃r�f�I�B�e�Ŋm���P�̑g�����f����
���S �u�Q�̕������v�̊�{�͓��䐔��H
�Q�̕����̃p���h�N�X�̌��_����(���̃x�[�W)

���z�����肵����@�Ŗ�蔭���I
���g�̌����Ȃ�������O�ɁA�ǂ����̕�����I�瓾���邩�H�Ƃ����̂��u�Q�̕�������v�̊�{�B�͂��߂ɑI�����Ǝc��̕����̊W�́A�P/�Q���m���ł������܂�Ȃ��B��ɂ��Ă�����z�Ǝc��̋��z���킩��Ȃ�����������Ă����Ȃ��Ă������B
�����邽�߂Ɍ�������ׂ����ƕ�����Ă��킩��Ȃ��B������A
point
�@�@�u�킩��Ȃ��v
���u�Q�̕������v�̐���
�u�������Ȃ��v�Ƃ��u���������v�Ƃ��͋C���̖�肾�����肷��B
�Ƃ��낪�A���̂����l���m���␔�w�̗��_�������o�����ƂŁA�P���Ȗ�肪�������Ă�₱�����Ȃ����Ⴄ�p�^�[���������B
����ȋ�ɁE�E�E�B
�҂đ҂āA�u�킩��Ȃ��v�ƌ��_���o���̂͂܂������B���̖������z�I�ȏ�����z�肵�čl�����@�ŊȒP�ɉ����ł���B���������������������Ғl���v�Z����A���̂��Ɠ��������o�����̂��B
���ɁA������������P���~�������Ă����Ɖ��肵�悤�B����ƁA�c��̕����ɂ́A�T��~�A���邢���Q���~�������Ă��邱�ƂɂȂ�A������̋��z���T��~���Q���~���Q�ʂ肵�����蓾�Ȃ����ƂɂȂ�B
�ł́A���̂Ƃ������Ғl���v�Z���Ă݂悤�B
�T��~�~�P/�Q�{�Q���~�~�P/�Q���P�Q�T�O�O�~
�����O���P���~���A�������邱�Ƃɂ���āA�P�Q�T�O�O�~�ɑ����邱�Ƃ����҂ł���B�������A����͌v�Z��̋��z�ł���A�������P���̎��s�̏ꍇ�ł���A�����邱�Ƃ����蓾��B�����A������J��Ԃ������ɁA��������Ғl�̋��z�ɋ߂Â��B
���̌v�Z�ɏ]���A���̋��z��������ł��낤���u�K�����������������ɂȂ�v�͖̂��炩�B
�Ȃ�قǁA���Ғl���v�Z���ăX�}�[�g�ɖ��������Ă킯���l�B�ł��A���z�I�ȋ��z�Ȃ畕���J���Č��Ȃ��Ă���������B�Q�l�̐l���ɁA���ꂼ��ʂ̕�����I������A�Q�l�Ƃ��������������Č����o���āA����������܂��������悤���Č����o���āA�܂��܂��E�E�E�E�A�Ȃ�Ă��ƂɂȂ�Ȃ��H
������w�E������肪�u�Q�̕����̃p���h�N�X�v�B
���z�I�����Ғl�̎����o�������ƂŃp���h�N�X���N���Ă���̂ŁA��̓I�ȋ��z�ɊW�Ȃ����ɏ��������Ă݂����B
�Q�̕����̃p���h�N�X�i��{�` + ��@���j
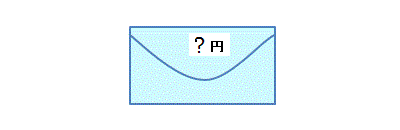
���������Ȃ��Q���̕����ɂ����������Ă�B���z�̊������P���Q�B
���������Ȃ���ԂŁA�I�����̒��̂��������炤���Ƃ��ł���B
������I��ŁA�c���������ƌ������邩�������B
�@�@�@
��@��
�P�A�I�����̋��z���`�~�Ɖ��肵�āA�c��̕����ɂ́A�O.�T�`�~���Q�`�~�������Ă���Ɨ\�z�����B
�Q�A���������������Ғl��
�O.�T�`�~�~�P/�Q�{�Q�`�~�~�P/�Q���P.�Q�T�`�~
�ƂȂ�A����������������������B
�R�A���Ɏc��̕�����I�����Ă����ꍇ���A�������ɂȂ�A����������������������B���ʁA�ǂ���̕�����I�����Ă�������������������������Ƃ����p���h�N�X���������Ă��܂����B
���@�ȏ�̍l�@�ŁA�p���h�N�X�̍��{�I�Ȍ����͂Ȃɂ��H
�����������ǂ��Ȃ�ƁA���̃p���h�N�X���������Ă��܂��B
����ȃg���b�N�ɘf�킳���悤����܂��܂�����ȁB�ǂ�Ȃ��̂ł����Ғl���v�Z�ł���Ƃ����v�����݂Ōv�Z�����Ƃ��낪�p���h�N�X�̌�������B
������������A�u�O.�T�`�~���`�~�v�A�u�`�~���Q�`�~�v�̑g���킹���Q��ނ����l�����Ȃ�����ƌ����āA���ꂼ��̑g���s���悭�ϓ����P/�Q���m���ŏo������ƌ��߂Ă����킯�ł͂Ȃ��̂���B�ǂ̂悤�ȋ��z�̑g��p�ӂ������ɂ��ẮA���ɐݒ肪����Ă����B�܂�A�o��҂̉�����m���Ȃ�����ł��ς���Ă��܂��Ƃ������Ƃ���B
���Ƃ��A�ŏ��ɑI�������P���~�������Ă����Ƃ��悤�B�I�����Ȃ����������ɔ��z���T��~�������Ă���\�z�͂Ƃ������A�o��҂��͂��߂���{�z���Q���~��p�ӂ�����肪�Ȃ��ꍇ�A�Q���~���܂߂��g�����Ɋւ��Ă��o�����O�ƂȂ��Ă��܂��B���R�A���Ғl�́A�O�ł���B
���̂悤�ȓ_���l���������Ғl�̌v�Z���̏o�����Ɏg���Ă���u�P/�Q�v�͖��m���Ƃ��Ă����K�v������B
���̂悤�ɁA�o�������s���ł���������Ғl�̌v�Z���ł����ɁA�����̑����Ȃǂ��s���̂܂܂���B�u�������ē����邩�킩��Ȃ��v����������B
�������A���ꂼ��̑g�����̏o�������P/�Q�ł���A�O�o�����Ғl�A�P.�Q�T�`�~���Q�l�ɂ��Č��������������ł���Ɣ��f�\����B
�u�Q�̕�������v�́A���ɓ�����Ɗ����Ȃ��āA���Ғl���v�Z����ΊȒP�ɉ�������Ǝv���Đi�߂�ƁA�K���p���h�N�X����������B���ꂼ��̑g�����̏o�������P/�Q�ł̓}�Y�C�ƋC�t���ƁA���m�������ăp���h�N�X���������Ȃ��悤�Ȏ����l���ĉ����B
�킩��͂��̂Ȃ��o����������Ɂu�P/�Q�v�Ɍ��߂Čv�Z�����̂��p���h�N�X�̌����B���m��������Ζ��͉�������B
�Ȃ�āA���M�����Ղ�̉�����Ă�l�����āA���̈ӌ��ɂقƂ�ǂ��u�ًc�ȁ[�����v�̗l�q�B
����ł����ɂ́u�Ȃɂ�����������ȁ[�v���Ďv���Ă�l���P�b�R�E���āA�J��Ԃ��c�_�ɂȂ�݂����B�����ł������������Ă��A�l�Ԃ̊��o�ł̓i�b�g�N������Ȃ����Ƃ��đ�����l�B���������̊��o�̕��������������肷�邩��ʔ�����_�B
�����A���̊��o�A�����I�ɂ���������
point
�u�Q�̕����̃p���h�N�X�v�́A
����ɍ��{�I�Ȍ����Ƃ�������
���߂ɍ������Ă���B
���������E�E�E
�Q�̕�������i��{�`�j�̒i�K�ŁA����������Ғl�́A�����̑O��ŕς��Ȃ��B�u�킩��Ȃ��v�Ɠ����Ă���p���h�N�X�͂Ȃ���l�B
�Ƃ��낪�E�E�E
�Q�̕����̃p���h�N�X�i��{�` + ��@���j�̉�@�ɏ]���Ė����������Ƃ���ƃp���h�N�X���������Ă��܂��B
���ǁE�E�E
���̑�Ƃ��āA�o�������u�P/�Q�v�łȂ����m�������ɂ�����A�ݒ�����낢��ς����m������������E�E�E�B
�u�Q�̕�������v�̌�Œ��ꂽ��@�Ńp���h�N�X���������Ă����A�܂��́A���̉�@�ɒ��ڂ��Ȃ���Ȃ�Ȃ��l�B
�����A���{�I�ȉ��������邽�߂ɁA��𑱂��悤�B

�u�Q�̕�������v�̖ӓ_���m�F���Ă�����
��ʓI�ɁA�育�킢�p���h�N�X�قǁA������Ƃ������Ⴂ���甭�����Ă��āA�����Ƃ͊W�Ȃ����Ƃ���b��ɂȂ�悤�Ȏd�g�݂ɂȂ��Ă�B�܂��A�u�Q�̕�������v�̊�{�ݒ���悭�݂āA�v�����݂⊨�Ⴂ���Ȃ����`�F�b�N���Ă������B
�܂����Ǝv���Ă��u���Ғl�v�Z�v����������
�莝���̋��z��m���Ă��܂���A�Ƃɂ��������u���Ғl�v���v�Z���đ������r���Ă݂����Ȃ�l�B���́u���Ғl�v�́A�ȒP�Ɍ����Ƃ���C�x���g�ōl�����錋�ʂƂ��̌��ʂ�\���������́B
���Ƃ��A�T�C�R�����P���U��C�x���g�ŁA���ꂼ��̖ڂ��o���m�����P/�U�ÂB�o���ڂ����P���~�D�����炦��Ȃ�ăI�C�V�C�b�Ȃ�A�N���肤�邷�ׂẴp�^�[���̌��ʂ�������������ׂāA�Ƃ肠�������v�����Ⴄ�B�����������������ׂ��p�^�[���̐��Ŋ�����P��������̕��ϒl�A�܂�u���Ғl�v���o����l�B
�P�̃C�x���g��������������ׂ��p�^�[�������v���p�^�[������
�v�Z�́A
���邢�́A�P�p�^�[�����Ƃ����Ғl�𑫂��������ƁA
�i�P�~�P/�U+�Q�~�P/�U+�R�~�P/�U+�S�~�P/�U+�T�~�P/�U+�U�~�P/�U�j���~
�����̌v�Z���Ɏg���Ă���u�{�v�ɒ��ڂ���ƁA�T�C�R���̏o���ڂ̃p�^�[������ׂāA���������v���邽�߂Ɏg���Ă���B�Ȃ�ő����Ă�̂����Č����ƁA���Ƃ��ƁA�S�̂��P�ɂȂ�悤�ɕ������ꂽ�m�����P�ɖ߂��Ă�낤���ă��P�B
point
�u�{�v���m�������v�o����̂́A
����̃C�x���g������
�T�C�R�����P���U��̂͊ԈႢ�Ȃ��P�̃C�x���g�B�����āA�P�̖����o��̂��U�̖����o��̂�����̃C�x���g���ŋN���肤�镡���̃p�^�[���Ƃ��čl���Ă���B���̏��������邩�炱���A�u�{�v�͂����̃p�^�[�������v�o���Ă���B
���܂�ɂ���{�I�����Đ����̈Ӗ����킩���B
��������l�B�u�{�v������̃C�x���g���ǂ����C�ɂ��Ȃ��Ŏg��������Ă�l�́A�`���v���J���v�������B�ŁA�������炪�d�v�ȂƂ������B�����A�u�{�v�̎g�p�������t��ɂƂ��ė��p������ǂ��Ȃ�Ǝv���H
���Ƃ��A����łȂ��C�x���g�A�T��~���P���~�̕����̑g�����ŋN���肤������p�^�[���ƁA�P���~���Q���~�̕����̑g�����ŋN���肤������p�^�[�����W�߂Ĉ��ՂɁu�{�v�ō��v������E�E�E
point
�u�{�v���قȂ�C�x���g���������āA
�ˋ�̃C�x���g��n�삵�Ă��܂��B
�܂�A�قȂ�C�x���g�ԂŁu�{�v���g�����ƂŁA�V�����������ꂽ�ˋ�̃C�x���g�ɏ����ς���Ă��܂��B���̌v�Z�͉\�ł��A����́A���O�܂ʼn������悤�Ƃ��Ă������Ƃ͍��{�I�ɕʂ̖��B
�u�{�v�̈ӊO�ȕ���p�ɋC�t���Ȃ��܂܁A�u�{�v���قȂ�C�x���g�ԂŎg���Ă��܂������R�̌��ʂ��u�Q�̕����̃p���h�N�X�v�����B���̓_�ɒ��ڂ���A�u�Q�̕�������v�̌�����������ɂ킩��l�B
���������C�x���g�͓����ʼn������ׂ�
�u�Q�̕�������v���m�����l����Ƃ��ɒ��ӂ��Ȃ���Ȃ�Ȃ��̂́A�u�Q�̕�������v�́A�O����V���ȕ����𑫂����Ƃ��������Ƃ��Ȃ��A������Q���������邾���̕����ꂽ�����C�x���g���Ƃ������ƁB
�ƂȂ�ƁA
point
�����C�x���g�ł́A���Ғl�����ϒl�ɂȂ�B
���Ƃ��A�`���a��I������I���C�x���g�ł́A�`��I�������ꍇ�ƁA�a��I�������ꍇ���Q�p�^�[�������蓾��B���ꂼ��O�������������Ȃ�A�I�����m���A���ꂼ���P/�Q�ł��邱�Ƃ����܂ł��Ȃ���l�B
�܂��A�`���a��������������C�x���g�ł́A�`���a�Ɋ�����Ɠ����ɁA�K���a���`�Ɋ����邱�ƂɂȂ邽�߁A�����Q�̃C�x���g�͑S�������m���Ŕ�������B�Ƃ������A�P�̃C�x���g���Ⴄ���ꂩ��Ȃ��߂��\���̈Ⴂ�ɂ����Ȃ��̂ŁA������m���P/�Q�ɂȂ�B
����ɁA�`���a�Ɍ������邩���Ȃ����Ƃ������f�ł́A�u���������v�Ɓu�������Ȃ��v���P�̃C�x���g�̕ʃp�^�[���ł����Ȃ�����A�K���g�ɂȂ����m���P���\������B
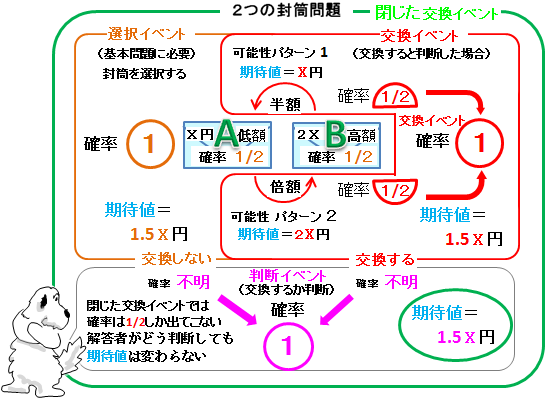
�u�Q�̕�������v�����������C�x���g�ł���ȏ�A�莝���̋��z���`�~�������Ɣ��������Ƃ���ŁA�g�ɂȂ镕���́A�O.�T�`�~���Q�`�~�̂ǂ��炩����Ƃ������Ƃ����킩��Ȃ��̂ŕ��ϒl�͋��߂��Ȃ��B
�O.�T�`�~�Ƒg�ɂȂ����m���P���\���ł���̂��`�~�������肦�Ȃ����A�Q�`�~�Ƒg�ɂȂ����m���P���\���ł���̂��`�~�����Ȃ��B�������m�����P/�Q�������蓾�Ȃ��ƂȂ�ƁA��z�]�~����ɂ����P.�T�]�~�Ƃ������ΓI�����Ғl���킩�邾���B
���ǁA�������Q�������Ȃ������C�x���g�́A�����̂��Ƃ͓����ŏ������ďz���邩���o���肵�Ȃ��B�P���̕����̋��z���s���Ȃ�A�������ē����邩���f����̂̓������Ƃ����A�����t�c�[�̍l�����������ł悳�������l�B
���z�̃r�f�I�B�e���m���P�̑g�����f����
�u�Q�̕����̃p���h�N�X�v�́A���Ғl�����߂�c�_������Ȃ��ɁA��{�I���m���̑g�����̘b�͂قƂ�Ǐo�Ă��Ȃ��B�K���ȃp�^�[����g�����Ėϑz�C�x���g������Ă���̂�����B�m���̋��ߕ����Ԉ���Ă���A���̌�̌v�Z���c�_���݂�Ȗ��ʂɂȂ�̂Ƀl�B
�u���������v�ꍇ�����ɒ��ڂ��Ă���u�Q�̕����̃p���h�N�X�v�́A�O.�T�`�~���Q�`�~�Ōv�Z�������Ғl���瑹���f���Ă���B
���̎��ɂ́A�m�������v������P�ɂȂ�悤�ɒ�������u���v�̑��݂��F�߂���悤�ɁA�u�O.�T�`�~�v�Ɓu�Q�`�~�v�̋��z��������̃C�x���g��z�肵�Ă���̂͊ԈႢ�Ȃ��������l�B�����āA���ꂪ�u�Q�̕�������v�̃C�x���g�ƈ�v���Ȃ����Ƃ��^���]�n�͂Ȃ��B
���̂悤�ɃC�x���g�őz�肳���p�^�[���̑g���������m�łȂ��ƁA���������̍l�@���������Ă̕��֍s��������߂��Ă���Ȃ��Ȃ�B����Ȃ��Ƃ��Ȃ��悤���m���̑g�������ȒP�Ɋm���߂���@�������_�B
���Ƃ��A�u�Q�̕�������v�ŗp�ӂ��ꂽ�Q�̕����ɂ����������P�̕�����I������܂ł��r�f�I�ŎB�e����B���̌�A�莝���̕������`�~���m�F���āA���Ғl�����߂悤�Ƃ����b�ɂȂ����Ƃ��Ƀr�f�I�������߂��čĐ����Ă݂�B������̃r�f�I�B�e�͑z����̘b�B
���F���z���������̃r�f�I�B�e�ʼn����킩��Ƃ����̂��B
�킩��ȁA���ꂪ�B�������A���z�̎B�e���O.�T�`�~���Q�`�~�̂ǂ�����ɓ��ꂽ���킩��킯�Ȃ��B�킩��̂́A
point
�O.�T�`�~���Q�`�~�̂ǂ��炩���m���ɁA
���Ƃ͂܂������W�Ȃ����z
���Ƃ������ƁB
�������Q�̒i�K�ŁA�u�`�~�v�Ƒg�ɂȂ�̂́u�O.�T�`�~�v���u�Q�`�~�v�̂ǂ��炩�Ƃ킩�����B�u�`�~�v�Ɓu�O.�T�`�~�v�̑g�������A�u�`�~�v�Ɓu�Q�`�~�v�̑g�����ł����Ȃ��B
������r�f�I�������߂��Ă��A�u�O.�T�`�~�v�Ɓu�Q�`�~�v�������o�Ă��邱�Ƃ͂Ȃ��B�o�Ă��Ȃ����z���g�������Ғl���v�Z����Ƃ������z�����͊���ƋC�t�����������ɂȂ�Ǝv�����ǃi�B
���z�̃r�f�I�B�e������̂́A�ǂ̎��_���m�������߂�ׂ������n�b�L���F�����āA���n�t�]���Ȃ��悤�ɂ��邱�ƂƁA���W�ȗv�f�����荞�܂Ȃ��悤�ɂ��邽�߁B�����ƊW�Ȃ�����r��������ʂ������_�B
�Q�̕������ǂ̂悤�ɏ������������d�v�Ȃ̂ł���B
�Ɗ�������A�܂��r�f�I���Đ����Ă݂�B
�������A�u�Q�̕�������v�̕�������������Ƃ���͉f���Ă₵�Ȃ��B�ݖ�ɖ�������l�B�Q�̕����Ɍ��肳�ꂽ��Ԃ����肪�n�܂��Ă���u�Q�̕�������v�̏����ݒ�́A�u���̖��ł͋��z����肷���|����͂Ȃ��v�Ə����ݒ肳��Ă���Ɖ��߂���̂��t�c�[�ɐ��w�I���Ǝv�����B
�����ݒ�����Ď��O�����������A���̌���m�������Ғl�ɉe�����o�邱�Ƃ͗e�Ղɗ\�z�ł���͂��B��������A�͂��߂���ʖ��Ƃ��Ĉ����̂���������Ȃ��H
�B�e����Ă��Ȃ������i�K�̘b��ɂȂ�����A��U�A�^����������āA�͂��߂���B�e���Ȃ������Ƃɂ��悤�B
point
�ݖ���ߋ��ɖ߂�ݒ�ύX������Ȃ�A
�������܂ł̃f�[�^�͏����Ă��܂����B
���O��������u�Q�̕�������v���ؖ����Ă��鐔�w�҂̘_���A�`���ŁA
�܂��A
����{�����Ƃ���E�E�E
�Ȃ�Ă���Ă��肵�Ȃ��H
�킴�킴�u�Q�̕�������v�̏����킩���Ă܂�����Đ錾���Ă͂��߂Ă�悤�Ȃ�����A��������ɂ���Ă��Ċ����B
�u�Q�̕�������v�̊�{�͓��䐔��H
�莝���̕����̋��z���킩��Ȃ���Ԃł��A���z�̔䗦���P�F�Q���Ƃ킩���Ă���A�P�F�Q�̓��䐔��̒�����A�������Q�̕��������o���āu�Q�̕�������v�̏o��Ɏg��ꂽ�Ƃ݂�ȗ\�z�����˃l�A�����ƁB
�@�@�@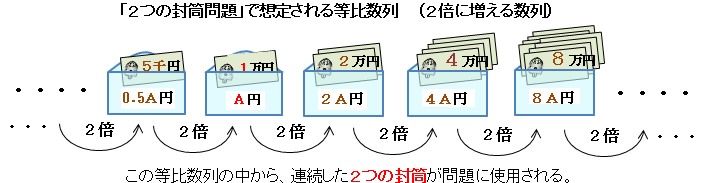
�o��҂����Ɏg���������Ӑ}�I�ɑI�����悤���A�܂������̖���ׂɑI�����悤���A���̓��䐔��̂����Q�̕����������u�Q�̕�������v�Ɏg���Ă��邱�Ƃ͊ԈႢ�Ȃ�����A���̓��䐔�����{�ɂ��낢��l����Ζ��͉����ł���Ɨ\�z�ł����l�A�����ƁB
�ĂȊ����ŁA���䐔��́u�Q�̕�������v�̊�{�`�Ƃ��đ傢�ɗ��p�����B�����̉\�����l����Ɠ��䐔�����I�����A�Ԉ���Ă�Ȃ�Ďv���Ȃ��B������u�������ē����H�v�ƕ������Ɠ��䐔�����������o�����m�����l���Ă݂�B
�ł��A�u�������ē����H�v�ƕ����Ă鎞�́u�Q�̕�������v�́A���炩�ɕ������Q�̏ꍇ�̉�v�����Ă����l�B�R���ȏ�Ȃ�u�ǂ�ƌ����H�v�ĕ����͂������B
���������A�u�Q�̕�������v�ł́A�͂��߂���I��܂ň�т��ĕ������Q���������݂��Ȃ��B�������Q���̕����̋��z��������ē��䐔��ƌĂׂ邩�͕ʂɂ��āA�����l���邽�߂Ɏg�����R���ȏ�̕����̓��䐔��Ȃ�āA�ǂ��ɂ����݂��Ȃ��B
�Ȃ�A�����ɗ��p���Ă��铙�䐔��͂ǂ�����N���ďo�Ă����̂��H
point
���������͉҂̓��̒��ʼn��z�����c��
�܂�A���䐔�������̏����ɂȂ����Ƃ��Ă��A����͍l�@�i�K�ł̘b�B���߂��Ă�����Q�̕����������Ƃ��Ă���Ȃ�A
point
�ɂ��̓��䐔����c���Ă͂����Ȃ�
���䐔��Ŗ����l����̂͗��ɂ��Ȃ��Ă��邵�A�ʂɖ��Ȃ��B�������A�����Ă��̏ꍇ�A�Q���̕��������Ȃ��u�Q�̕�������v�ɁA�l�@�Ɏg�������䐔��̕������ǂ�ǂ�lj����āA�]�v�ȉ��o���Ă��܂����Ƃ������B�ӊO��������Ȃ����ǁA�u�킩��Ȃ��v�Ƃ����́A���䐔����c���Ȃ����z�I�ȉƂ�����B
���̕ӂ́A�قƂ�ǒ��ڂ���Ȃ��҂̉v���Z�X������������Ȃ������B�҂������l���邽�߂ɓ��̒��ŕ`�������z�I�ȓ��䐔�u�Q�̕����̃p���h�N�X�v����蕡�G�ɂ��Ă���Ƃ����F���������āA��蒍�Ӑ[���l�@����K�v������l�B
�݂�ȁu�������Q��ށv�����炵�Ă���
�����̖������@���A���䐔��̒�����A�������Q���̕������T���v���Ƃ��Ď��o����Ƃ��@���̒��̉��z�C�x���g�Ƃ��ĕK�����s���Ă�͂��B�����āA�u�Q�̕����̃p���h�N�X�v�ŁA���̎��o��������̓I�ɒ����ƁA���̃C�x���g�ׂ͍�����������Ď��{�����B
��@�@�P-�P
�I�����̋��z���`�~�Ɖ��肵�āA�c��̕����ɂ́A�O.�T�`�~�������Ă���Ɨ\�z�����B
�莝���̋��z��\�z�����@�������ƁA�����A�莝���̔��z�̕����Ƒg�ɂ����T���v���䐔����o���Ă݂�B
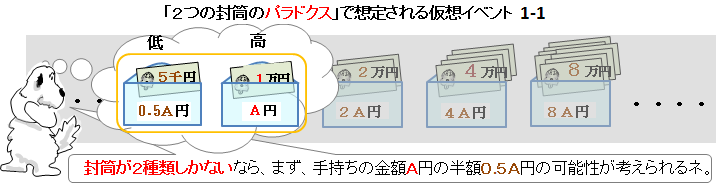
�i���̉��z�C�x���g�P-�P�ł́A�������Q��������c��Ȃ��B�j
��@�@�P-�Q
�I�����̋��z���`�~�Ɖ��肵�āA�c��̕����ɂ́A�Q�`�~�������Ă���Ɨ\�z�����B
�����āA�����P�̉\���Ƃ��āA�莝���̕����̔{�z�̕����Ƒg�ɂȂ�T���v�������o�����ƂɂȂ�B
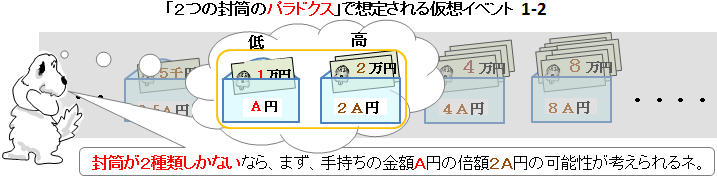
�i���̉��z�C�x���g�P-�Q�ł��A�c���ꂽ�������Q������邱�Ƃ͂Ȃ��B�j
�����܂Œ��ꂽ��@�ɏ]���ĉ������ʂȂ��Ƃ����Ă��Ȃ��悤�Ɏv����l�B�ł��A�����ŗ�ÂɂȂ��čl���Ȃ���Ȃ�Ȃ����Ƃ́A�P����̗\�z�C�x���g���I���������A�{�z�̏ꍇ��z�肵���Q����̃C�x���g�����{������A���̏��Ԃ��t�̏ꍇ�ł��A�Q���̃C�x���g���Ɏ��s���Ă��Ȃ��Ƃ��낾���B
�u�Q�̕����̃p���h�N�X�v�̉�@�ł́A�P���̃C�x���g�����S�ɏI����Ă���A�d�蒼���ŕʂ̃C�x���g�����{���邱�ƂŁA�����܂Łu�Q�̕����v�̏���������Ȃ���@�ɂȂ��Ă�B
�����A��̕����𒆐S�ɂ��ĕ������R�I�����Ă��܂��ƁA��ȊO�������P�̕����́A��̋��z�̔��z�ł���A���{�z�łȂ��Ɓu�Q�̕����v�ł͂Ȃ��Ȃ��Ă��܂��B�ł��A����ȕ����Ȃ�Ă���킯�Ȃ�����A��@�ł́A�������Q���ȏ�ɑ����Ȃ��悤�ɁA���ꂼ��̃C�x���g�����S�ɕ����Ă���B
�܂�A��@�ɏ]���ăC�x���g�����z���Ă��鎞�_�ŁA
point
�҂́u�������Q��ނ����Ȃ��v���Ƃ𗘗p���Ă���B
�Ƃ������ƂŁA�ǂ�Ȃɂ����Ƃ��炵���ł��A�������������R����ȏ�o�Ă���̓A���G�i�C�B�����������Q��������Ȃ��ꍇ�̓����𗘗p�������������d���Ȃ��l�B
���z�����z���āA�݂�Ȃ�����Ă���]�v�Ȃ���
�莝���̕����ɓ����Ă�����z��m��Ȃ������u�Q�̕�������v�̎��_�ł́A�������Q���ŁA�����邩�����邩���킩��Ȃ��B�Ȃ��Ȃ�A�I�����ƑI�Ȃ����������̑��ΊW�͊m��ł��Ȃ�����B
�ǂ����̋��z���������킩��Ȃ����炠����܂����l�B
�Ƃ��낪�u�Q�̕����̃p���h�N�X�v�ł́A��̓I�ȋ��z�Ɍ��炸�A���z�I�ȋ��z�ł��A���������������Ғl���v�Z�\�ɂȂ�Ɛ�������Ă���B
���z�I�ȋ��z��z�肷������Ғl���v�Z�\�ɂȂ�B
�����̒��g�����邱�Ƃ����Ғl����������͓̂��R����B
�قƂ�ǂ̐l�������ƍ��{�I�ȁA�X�J�b�g����悤�ȃg���b�N�Ƀ_�}����Ă��邱�Ƃ����҂��Ă����͂��Ȃ̂ɁA�����ȉ���Łu���O�m���v��u�����t���m���v�Ȃ�Đ��I�Ȑ������悭��������B���p����ׂ��������K�v�������Ȃ�āA�t�Ɂu�Q�̕�������v�̖��͂�������������������B
�N�C�Y���o�ł������������̃V���E�g�̓`���v���J���v���Ȃ���A����ł��������肵�Ȃ��B�ǂ�Ȃɐ�������ׂ��Ă��A�{�\�I�ȁA�E�[�b�Ă��Ȃ肽���Ȃ銴�����c��̂͂Ȃ�ł��낤�l�B
�I���z�ƑI�Ȃ��������z�̑��ΊW�����Ă���u�Q�̕�������v�ŁA����̋��z�����z���Ă݂������ŁA���ΊW���𖾂ł����Ⴄ�̂̓i�[�H
���z�̉��z�ȊO�ɁA�Ȃ]�v�Ȃ��Ƃ��Ă����炶��Ȃ��H
�莝���̋��z�����肵��������āA�Q���̕����̑��ΊW�ɕω����N����킯����Ȃ����A�V�������̎�|����ɂȂ�킯�ł��Ȃ��B���ꂾ���ŁA�����f���鑊�ΊW�����I�ɉ𖾂����̂͂ǂ��l���Ă��I�J�V�C�B
�����ŁA���z�����z�����Ɠ����ɉ����N���Ă���̂���͂��Ă݂�B
���z�C�x���g�P-�P�����z�C�x���g�P-�Q�͓����ɐ������Ȃ��C�x���g������A�����҂����ꂼ���P�Ƃʼn��z�����Ƃ���B
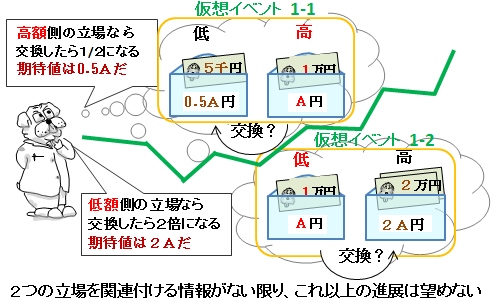
���̂Ƃ��҂́A���z���`�~�̕����������Ă���Ƃ������ʂ̐ݒ���������C�x���g�Q����z�肵�Ă��邪�A�����̃C�x���g�ɒ��ڂ̊֘A���͂Ȃ��B
���̏����̂܂܉ɗ��p�����Ƃ��Ă��A���ꂼ�ꂪ�u�킩��Ȃ��v�Ɠ����Ă���Ή������͋N���Ȃ��͂��B
�I�b�B�Q���̗���`�~�̕����������Ă��闧��́A���S�Ɉ�v���Ă�ł͂Ȃ����B
������i�j�H�@��߂ăl�B�]�v�Ȃ��ƍl����́B
�ǂ��_�ɋC�t�����B�ł���A�莝���̕����𒆐S���A�O.�T�`�~�A�Q�`�~�̓��䐔������Ғl�����߂邱�Ƃ��\����B
�������߂Ă��Č����Ă���ǁB�]�v�Ȃ��Ƃ���́B
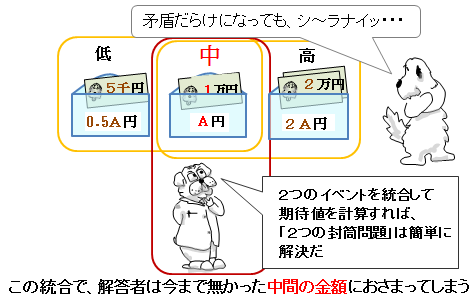
�A�b�B�����������B
�莝���̋��z���牼�z���邾������Ȃ������̂��i�@�E�E�E�B
���S�ɓƗ����Ă����C�x���g���P���ɓ������āA�莝���̕����͂��������荂�z�A�莝���̕����͂����������z�Ƃ����Q���̈قȂ鑊�ΊW�܂ł��������Ă��܂����B
���̌��ʁA��z�A���z�A���z�A�R����̋��z�������ɍ��݂��镕���̃T���v�����o���オ�����B�Ɠ����ɁA�莝���̋��z�䐔��̒��ԋ��z�ɌŒ����āA�N������ł��Ȃ��ݒ�ɕύX���Ă��܂����B
���ꂱ�������ΊW�̕s���ȁu�Q�̕�������v�ɁA���̊Ԃɂ����ΊW���m�肳��錴���Ȃ�_�B
point
�҂͋��z������i�������J���j����C�x���g�ŁA
�R��ނ̕����Ƒ��ΊW��n�����Ă���B
�����炭�A�u�Q�̕�������v�͒��N���Ⴂ����Ă��Ă���B�����č��ł��B�҂�����Ă邱�̓����C�x���g�Ɋւ��ẮA�m���_�������o���O�ɍl�@���ς܂���ׂ��Ƃ���B�Q���I�Ȗ��ł����Ȃ��m���_�Ńp���h�N�X���������悤�Ƃ���ƁA�����ǂ��납�ǂ�ǂG�����Ă��܂�������A���b�p���u�Q�̕�������v�́A���҈ȏ�ɖʔ����l�B
���̓����C�x���g�̉e�����ǂꂾ���傫�����A���̌����͂𑱂��邱�Ƃɂ��悤�B
�\�z�O�ɒ����Ȃ�����ŁA���̑����́A