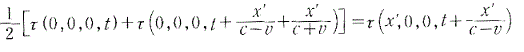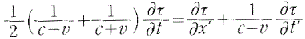勘違いだらけ、前野昌弘氏の批判文の場合

本物の色物物理学者たち特別編
§４ 日高守・『相対論を打ち砕くシルバーハンマー』

　　　　　　　　　　　　　　　　　　以下、本物の色物物理学者たち特別編より引用、抜粋

著者の日高氏は、相対論の数学がおかしい、と文句をつけている。『なぜ物理学者までもが小学生でもわかる数学トリックに騙されてしまうのでしょうか』という具合だ。

その数学トリックは、「関数である物を関数である事を忘れている」という事らしいのである。そして、その“本来関数であるもの”を相対論を打ち砕く物、という意味で「シルバーハンマー」と呼んでいる。（なぜシルバーなんでしょう？アインシュタインを狼男かなんかと間違えている…なんておことはないわな。）

ビートルズを聞き込んだ人なら「マックスウェルズ シルバーハンマー」の歌詞が元になっていると気づいて、「シルバーハンマー」が打ち砕くのは相対論ではなく、「おごりたかぶり」だとわかるはずです。（詳しい解説ページは現在作成中です。）

本文全体では、

ということを主張しています。

相対論が正しいと信じるあまり、これらを検証もしないで批判すると、

と警告しています。

では、前野昌弘氏にお贈りする「シルバーハンマー」を見てみましょう。

まず一つ目は E=Mc² について、『一般に知られているような重要な意味を持っていない』と主張しています。

まずアインシュタインの論文『質量とエネルギーの等価性の初等的証明』という論文に関し、『実験データを一切用いずに、仮想実験だけで E=Mc² を導き出しています。常識的に考えてデータを見ないで関係式を導き出せるはずがありません』と主張しています。

ところが、このアインシュタインの論文（日高氏は1905年の論文と書いていますが）は、1945年の論文なのである。1945年と言えば、もう相対論ができて40年。つまり、相対論に関する実験データなどが揃いに揃った後で「 E=Mc²だけど、こんな簡単な証明もあるよ」と補足するために書かれた論文なのである。「実験データもなしに」という批判はまずこの点で的外れだ。

また、理論だけから式を作る事自体は、別に不思議でもなければルール違反でもない。日高氏は「こうだとするとこなる。実際にそうなるかどうかは実験で確かめよう」という論文には存在価値がない、とでも言うのであろうか。

本文中で実験データを使わずに「比率」が出せないと何度も説明しているので、ここを勘違いする人はいないと思っていましたが、理論から式を作ることを批判していると勘違いしています。当然ながら、ごく一般的な手法を否定しているわけではありません。

よく科学史を延々と述べる人がいますが、議論のテーマが歴史的背景や物理的妥当性と直接影関係ないなら、先に論点を理解してからにした方がいいと思います。この場合「ところが、・・」の後で歴史的背景と一般論へと話がそれ、あさっての方へ行ってしまいます。

実験データがない論文の何が問題なのか、証明している対象がわからなければ批判できないはずです。

ここで注意すべきは、

ということです。

アインシュタインのE=Mc²を評価するには、物理面でなく数学的にまだ未発表の成果を使わなくてはなりません。データを使わずに比率を算出するという、誰も見つけたことのない数学の手法を要求しています。ここが本当の論点であるとわかれば、物理的考察の出る幕はないのですが・・・。

計算についてのコメントの後、日高氏はこんな事を言っている。

「E=Mc² は仮定した物理的意味を記述しただけの理論式にすぎません。量的要素をまったく含んでいないので、単位や数値を入れて使う事はできないのです。（中略）論文のどこにも単位や量を設定している箇所はありません。（中略）この点に気をつけて E=Mc² の意味を説明すれば、『質量の単位と C² 倍大きいエネルギーの単位 E でエネルギーと質量の等価性を仮定すれば E=Mc² となる』なんとあたりまえなんでしょうか。」

そら、あたりまえでしょうけれど。

物理の論文で単位が省略されているのは、組み立て単位を使っていると思ってくれ、という意味なのである。

物理の習慣に慣れすぎると、今までにないものを証明している論文でも同じように単位を使えると勘違いしてしまいます。

前野氏は、何も考えずにアインシュタインの論文でも組立単位が使えると考えているようですが、ここは完全な誤りです。

言うまでもないことですが、組立単位はすでに関係のわかっている物理量について話を進めるときに、「今は単位のことは気にしないでいいよ」という時に使います。つまり、論文のはじめから状況が分かっている場合です。

『質量とエネルギーの等価性の初等的証明』では、はじめから組立単位を使う設定になっていません。最後になって変換比率を示すことで量的関係を証明しているからです。組立単位が冒頭から存在していたら証明でなく、単なる応用例でしかなくなります。

ですから、E=Mc²の論文で単位は省略されているのではなく、はじめから存在させるわけにはいかなかった論文なのです。

例えば、Mに[kg]、Cに[m/s]を使ったのならエネルギーの単位は[Kg・m²/s²]（これはMKS単位なので、ジュールに等しい）になるし、Mに[貫目]、Cに[ヤード/時]を使ったのならエネルギーの単位に[貫目・ヤード²/時²]（こんな変な単位はもちろんないが、作ろうと思えば作れる）を使う、というだけのことだ。どの単位を使っても E=Mc² は成立する。

そもそも、 E=Mc² 自体、核分裂の際のエネルギーなどで実証を得ている、という事実をこの人はどう考えているのであろう？？

一番多いのはこのての勘違いです。

アインシュタインが最後に単位同士を変換する未知の係数を求めなくてもいいように、E=Mc²を示す直前で一般化をしている個所があります。これを見逃している人は、結果だけを見てE=Mc²がどの単位でも成立すると勘違いする場合が多いようです。

論文の最後しか見ていないために、単位系を並べて検算をしてみるものの、論文全体の流れを追うと簡単に否定できてしまいます。

Ｍ´−ＭがＭになるように仮想実験のパラメータを調整すれば、E=Mc²のような単純な式に変形できるということです。質量の増加分に対してどのくらいエネルギーが増加したか、この一般化によって未知の変換係数は棚上げにされた状態です。

この直後で論文が突然終わっていることから、アインシュタインはこの結果が衝撃的な結果を証明していると勘違いしているようです。実際は、

アインシュタインや一部の物理学者は、付加定数を１にして省略してしまうと、物理量を評価できなくなることを知らなかったと考えざるを得ません。このまま論文の評価も終わっていれば間違いとは言えなかったのかもしれませんが・・・

前野氏のように、この結果に対して、実験データや単位を直接入れてしまうと、実験待ちになっていた未知の変換係数は棚上げから一気に１とみなされて省略されてしまいます。本来はどんな単位を使おうと、未知の変換係数が式に追加され、それを実験で確かめればいいだけです。

また、組立単位を使えるなら、論文がなくてもエネルギーと質量の変換比率に合わせた単位がすでに存在しているということです。なにも変換比率を証明した論文の最後の段階で既存の単位を使わなくても、仮想実験の冒頭からすべての式で使ってもいいはずです。

あと、E=Mc²は、あらゆる物理現象と何の関係もない式だと考えています。理由は以下のページで。

次に日高氏が文句を言っているのが、アインシュタインの「運動している物体の電気力学について」という論文について。

日高氏は、アインシュタインの論文の数式の中で、

が

と変形されているのを見て（両辺をx'で微分して、x'を0と置いただけなのに）、上の式ではτは（）のついた“関数”だったのに、下の式では“関数”でなくなっている！と批判しているのだ。

『ここで何が行われたかというと、「関数の括弧と倍数に付ける括弧とを間違って中身を計算してしまった」または「未知関数τを一次関数の求め方で出してしまった」のです。』

ほんとにアインシュタインがこんな事をやったのなら、小学生にも笑われるだろう。しかし、ここでは単に省略しただけで、τが関数であることをアインシュタインが忘れたわけではない。そんなことは普通の人なら明らかだと思う。

日高氏は下の式のτに微分記号がついていることをどう考えているのだろう？アインシュタインは関数でない物を微分するほど数学ができないと思っているのであろうか（思っているかもしれないなぁ）。

本文中で「未知関数を求める公式が存在しなくても関数τが求められたのは間違った方法を使ったからです。」と書いているように、少なくとも関数τが未知の関数であること強調しているので、

という点が論点になり、これを考察してから先に進むはずですが、

と、論点を飛び越えたことを言っているので、関数τが未知関数であることすら気づいていない、あるいは、未知の関数でも微分すれば答が出せるという考えのようです。

微分は方程式の変化の割合を表現する方法ですが、関数の方程式が分からない状態では何の役にも立ちません。アインシュタインが求めようとした関数τは、運動する座標系でどの様な時間の変化をするのかを求める前に文字τで代替したもので、実験データや別の理論で穴埋め予定のものです。

このような本来は求められるはずのない未知関数の解を求める方法として、「関数の括弧と倍数に付ける括弧とを間違って中身を計算してしまった」ことを本文で指摘しましたが、これは未知関数を係数として処理する相対論独特の展開方法です。

未知関数τを微分するということは、基準になる関数が判明しているということですからこの時点で未知関数ではなくなります。しかし、データが増えているわけではありません。未知関数で止まっていた展開を微分係数に変化させて強行突破しているだけです。

展開方法としては致命的な誤りになります。微分に限らず、その他どのような演算であっても、未知関数の括弧の数を変化させたままなら、その手前で未知関数であることを忘れた証拠になります。「それ以降の式は難解で理論の正否を判断するにはあまり参考にならないでしょう。」と書いたのは、この誤りで相対論が関数τを見失い、解決不可能に陥っているからです。

さて、この後、例によって「光速度不変の法則」に文句を言い始める。いわく、

「ある特別なカメの歩く速度が誰から見ても一定と仮定します。『カメ速度一定の法則です。ここであなたは世の中の物理法則をこのカメに引きずられるように習性しなければならないと結論するでしょうか 』」

光速度は実験で一定とわかっているが、そんな変なカメは誰も見つけてないぞぉ〜。見方によって速度が変わって見えるカメならいくらでもいるけれど。 　相対論の本はたいてい、光速度一定の話から入るので、光速度一定だけが相対論の前提だと思っている人はけっこう多いかもしれないが…実際には、電磁気の基本法則であるマックスウェル方程式が動きながら観測する人にとっては（相対論なしには）成立しない、という事も大きいのである。つまり、電磁気学の諸現象はすべて、相対論の証拠なのだが…。

当然ここは、

について考察しなければならないところです。時間と距離の同じ「速度」になる組み合わせは無限に存在します。無限にある組み合わせが相対論の基準になっているということが分かっていないと、光こそが特別な存在だという感覚で物理法則の中心に据えることになります。

そして、

わざわざ特殊なカメがいると仮定した場合にもかかわらず、「速度」が基準になっていることを理解できていないため、カメのような「対象」では相対論の基準にならないと判断してしまうようです。光や電磁波が「対象」なら多少変動しようと、解釈を変えてでも受け入れようとするでしょう。

もし、「対象」が光に限定されるなら、本文で指摘しているように光を特別な基準にした式「ｃ＝１」「ｆ（ｃ）」で完結します。光速度不変の原理をそのまま「速度」基準の数式に取り入れた相対論では、関連した現象すべてが原理に引きずられる理論構造になっていて、秒速３０万kmになる「対象」を光に限定している部分がどこにもありません。そのため、同じ「速度」ならみな同一視され、カメであろうと基準になり得ます。

ということは、相対論における光速度のの持つ重要性はなくなり、電磁気学との関連性も希薄になります。

アインシュタインはマックスウェル方程式がローレンツ不変になることを念頭に置いて相対論を構築したはずです。それら構築材料が相対論の証拠になると主張している物理学者は珍しいのではないでしょうか。

また、ガリレイ不変でないマックスウェル方程式について疑問に感じていないのも不思議です。ローレンツ変換が不完全なガリレイ変換で現れる修正係数であることを知っていれば、ガリレイ不変になる式を考察したくなるのが科学者だと思うのですが、挑戦してダメだったのか、そういう発想ができなかったのかは不明です。

いずれにしても、電磁気学の不変性と相対論の共通点は不完全なガリレイ変換によってローレンツ変換係数が発生している点であり、基本になるべき座標系については根本から異なっています。絶対空間を想定したマックスウェル方程式をローレンツ変換すれば、相対論の主張している時空と同じよう歪むだろうと考えるのは誤りです。

この後、マイケルソン・モーレーの実験について、「動きながら実験しているのなら、鏡を傾けなくてはいけない筈だ」というよくわからない論拠の後で、式の計算を完全に誤解していますが、長くなってきたのでこの項はここまで。

文句つけると切りがないんだよなぁ…ほんとに。

運動系で斜めの光線が光速度不変で速度ｃになると確定した後であれば、ハーフミラーでどの方向に反射させようと運動系から移動しない限り速度ｃは変化しないはずです。そこで光線が真上に向くように作図すると、装置の光路長に収まりきれずに飛び出してしまうというのが本文の指摘です。

つまり、運動方向に垂直なy軸方向成分について、相対論的変換から除外されていることがy軸方向の整合性を崩しています。

相対論的な作図が光速度不変を満たしているように錯覚するのは、あくまで静止系と運動系の変換係数を数式にゆだねる前提があるからです。幾何学的に辻褄が合っている図ではないので、実際の装置に置き換えた作図すると、係数や暗算で処理していた部分が浮き彫りになります。

多くの相対論解説の作図に共通する誤りですが、速度ｖについてガリレイ変換をそのまま採用することで、斜めの光線を創りだし、相対論が確定するまで仮の変換を代替しています。このとき速度ｖは相対論的変換を免れています。

相対論の係数が、cでなく観測者の速度ｖに依存して変化するのは、最後まで代替していたガリレイ変換を削除できなかったからです。

と、ここまで補足説明です。本文では仮想的な幾何学処理によって光速度不変を否定した後、ハーフミラーが「正確に４５度の角度を保っていたと結論」しているので、

というのは、上記の幾何学的操作を物理的操作と勘違いしたのでしょう。ただ、本文の図と説明が適切だったかというと、説明不足の感は否めません。

マイケルソン・モーレーの実験を引用する相対論の解説の多くでは、ニュートン力学の矛盾を指摘した後でローレンツ変換式を求めるという構成ばかりが目立ちます。光速度不変の条件下で干渉縞は当然観測されないだろうと、軽く触れるか、あるいはまったく検証しないのが通例です。

たしかに、光路長も光速度もまったく同じなので、光速度不変の場合は検証する意味はなさそうです。ところが、この実験で作図までしてあるのに一番見落とされてる反射の法則を考慮すると状況が変わります。本文で示したように相対論の立場からマイケルソン・モーレーの実験を検証すると意外な発見があるかもしれません。

たとえば、相対論によれば静止系で反射の法則が成立するなら、運動系でもまったく同じように成立するはずで、静止系で真上に反射した光線は、運動系でも真上に反射して見えます。これが進行方向に介在する相対論的収縮係数の当然の結果だとすれば、

つまり、変換係数は不要です。光速度不変と相対性原理を両立させると、光の運動に関して相対論的変換はおろかすべての座標変換を受けつけられなくなります。光速度不変にすると変化がなくなるので相対論が不要になるのはしかたないです。

もっともとマイケルソン・モーレーの実験式自体に誤りがあるので、相対論の導出は不成立になります。これについては　「実験式を修正しよう！ 」　でマイケルソン・モーレーの検証式を修正しているので省略します。

前野氏の批判に見る反相対論批判の問題点

戦いでなく科学を

相対論をめぐる議論では、「相対論はまちがっている」という意見を疑似科学扱いする論調が大半を占めています。アインシュタインと絶対的多数の支持を得ていると確信すると、過激な批判を自慢げにする人たちが現れます。

前野氏も物理学者という立場を利用して「色物科学者研究編」で、「本物の色物物理学者たち」を一方的に批判（というよりバカに）しています。おそらく相対論を教えている専門家の立場を守るために、、相手にダメージを与えて歯止めをかけようとしたのでしょうが、物理学者の発言にしてはあまりにも無責任です。

中でも「かがくのおはなし」では、子供たちをあおりたてて攻撃へ仕向けるという信じがたい内容になっています。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　かがくのおはなし　より引用、抜粋

超科学と戦うための７個の式

君にはあるか？　もはや科学とはいえない虚しい議論を読み続ける根性が。
君にはあるか？　愚かにも超科学に引き込まれた友を諭す友情が。
君にはあるか？　理不尽な論理と事実の誤認に対する怒りが。
君にはあるか？　全てを陰謀で片付ける事への嫌悪感が。
君にはあるか？　超科学に立向かう勇気が。
＜中略＞

超科学のしかける最も甘い罠、それが「相対論はまちがっている」だ。
このローレンツ変換の式の簡単さが、超科学者のつけ込むところだ。
だが信じよ。単純な式の中にこそ真理のある事を。そして、マイケルソン・モーリーの実験が正しいことを。
　　　　　　　　　　　　　　　　　　　　　　　　　　　＜中略＞

世界から超科学が消え去る日まで、戦い続けよ、真理と科学の勇者だち！

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　92' Aug. いろもの物理学者と愉快な仲間達

カルト的な思想コントロールで大勢の一般人が犠牲になった科学テロを連想する人もいるでしょうが、これは大学の教員が書いた文章です。しかも本人は愉快だと感じているようです。

科学の世界で戦うという言葉は議論を指すことがありますが、真理のためにニセ科学や超科学と戦っていることを強調している物理学者ほど、利権を脅かす敵にダメージを与えるのが目的だったりします。WEB上で特に相対論支持者の行儀の悪さが目立つのも、このような科学教育が浸透しているからでしょう。

科学者の役割は決定論や思想の押し売りではなく、自然からいかに謙虚に学び取るかを主導し、科学倫理を十分理解した立場から道を踏み外すことが無いように見守ることだと思います。

反相対論を攻撃をする勇者（自分）や、敵視した相手に攻撃を呼びかける手法は科学ではありません。異論に対して反論し、反論に対して議論を重ねることで、科学はより洗練されてゆくはずです。要するに、

と思います。

正直めんどくさい

だいたいにおいて、正義を振りかざして戦いを先導する首謀者は、身の危険を感じると自分だけ安全なところへ逃げ出すのが常です。

前野氏の場合も科学者の力を誇示しようと批判文で虚勢を張ったものの、デタラメな内容を指摘されてへこんでしまったようです。「要旨に合った反証を示してはいかがでしょうか。」と、見直しを打診していましたが返事は来ません。

ツイッターでは・・・

迷惑な記事の見直しをお願いしただけで、たとえ相手が擬似科学者であろうと悪態をつくようなメールを送ったことは無いのですが・・・。被害者を装ってまで逃げるくらいなら、はじめから批判しなければいいと思います。

（ちなみに、本HPでは、事前に本人とコンタクトを取ってから掲載するようにしています。）

反証できないなら相対論を教えないでほしい・・・

時空が曲がり時間が遅れる、ＳＦのような相対論を信じるのは勝手ですが、それを生徒に教えるとなると事情が違います。根本から信頼に値する理論だと確証を挙げられないなら、生徒に嘘を教えていることになります。

生徒さんは、もし、先生がもっともらしく双子のパラドクスや時空の収縮を語り始めたり、相対論のテストで減点されたら抗議するべきです。

相対論を指示する物理学者の大部分が、電磁気学とローレンツ変換の結びつきから、相対論の必然性を確信しているようです。しかし、なぜ電磁気学でローレンツ変換が出てくるのか物理学者は誰も説明できません。

と言う答を鵜呑みにしていたのでは、永久に相対論から脱出できなくなります。

歴史上、ローレンツ変換の導出法はいくつか「発見」されていますが、それらはどれも二次的な応用例に過ぎません。数学の表記法に関するいくつかの誤謬を組み合わせることで、未発表の導出法はいくらでも創作することもできます。また、逆に理論に現れるローレンツ変換を演算の誤謬だけで再現することも可能です。

例えば電磁気学の場合、マックスウェル方程式をガリレイ変換したものが不変にならないことからローレンツ変換の必要性が主張されていますが、マックスウェル方程式の中にあるベクトルどうしの掛け算を演算記号で表現したことで、この演算部分がガリレイ変換を免れています。

不完全なガリレイ変換を修正するための逆変換がローレンツ変換です。自然法則と無関係な誤謬を物理学の理論と勘違いしている物理学者の特徴は

おそらく、想像もしたことがないほど単純な誤りにとぼけるしか手はないでしょう。

ローレンツ変換がどの様な仕組みで導出（発生）するのかをよく理解していれば、ここから絶対座標を飛び超えて時空を歪める理論が構築できると考えることもないでしょう。数学の基礎を見直さずに、反相対論を批判しても無駄です。

教えている生徒さんには、相対性理論に入ってからより、その導入部分の説明が必要でしょう。

これらの根本的な問題は数学的に解決できるものです。

現在の物理学はすべて絶対座標で構築されています。絶対座標から伸縮する座標に移行したはずの相対性理論も例外ではありません。ローレンツ変換を導出した後で絶対座標を否定できるという考えも、基礎ができていないのか

氏が積極的に公開してる相対性理論の講義ページにも誤りが多数あります。おそらく、実験事実をローレンツ変換で修正することと、相対論の実験実証を混同しているのだと思います。

数学的反証を示せないなら、大学で空想科学を教えるのは控えてほしいものです。