トリックの概要
相対論の決定的な間違いは、
光速度cを暗算で一定値に修正してから理論を始めたことだよ。
アインシュタインは、ニュートン力学で光速度不変の原理を考えて、
光の速度は誰から見ても一定値cなのだ!
一定値c光速を計算する必要などない
ってことで光速度cを暗算で出していた。
そもそも、ニュートン力学を否定しているのに、「誰から見ても」の部分で、
おもいっきりガリレイ変換を使うしか選択肢がないヨネ。
光速度不変の原理がガリレイ変換を使った後でも成立する方程式を求めるなら、
τ(運動系の光速度)=c
のように、求めたい方程式を
未知関数τの形で残しておいて、
それを解けば、
τ(C−v)=C−v+v=c
光速度不変の原理が実はvを足すだけの関数だってこともわかる。
この暗算に該当する文字を式に記入しとかないと、式を作った時点でこの分だけ差が出てきてしまう。アインシュタインのように定数として光速度cを扱ってしまうと、
point
原理で使った暗算が永久に文字cの中に閉じ込められてしまう
人類の物理学史上、誰も見たことのない数学トリックの完成だヨ。そんなことなど予想もしていないアインシュタインは、
光速度cが一定になるような未知関数τを定義して、
古典物理学の時空をゆがめてしまえばよい。
ってやっちゃったもんで、「特殊相対性理論」のモーソーの世界が始まったってワケ。
こういった初期設定の問題を考えようともしないで、
なんて主張している専門家たちが、理論物理学をゴミだらけにしてる。
こんな単純なトリックで
100年以上脱線している現代物理学!!
いったい誰のための科学ナンダロ?
最初に確認しておくよ。
問 題
光速度不変の原理というのは、
「だれから見ても光の速度は一定に見える」ということ。
そのためには今とは違う別の立場に移動して、
「やっぱりこの立場でも光速は一定なんだ。ヘェーッ」
とナットクする必要があるネ。
つまり、この原理を想像するには、別の座標系に移動する座標変換を使わないと評価できないという大前提があるんだ。
じゃあ、みんながこの原理を思い描くときに
自然に使っている座標変換はどっち?
相対論の式を知らなくても光速度不変の原理を想像できるのは、昔からみんなが使っているガリレイ変換を無意識に使っているから。ここでもし、ガリレイ変換以外の変換式が必要なら、相対論の構築後でないと光速度不変を評価できないことになる。
アインシュタインは光速度不変の原理を相対論の初期設定に取り入れてからローレンツ変換を導出しているので、求められる前のローレンツ変換を使うのはアインシュタイン本人でも不可能。ローレンツ変換は、ガリレイ変換を適用した実験の隙間を埋めるために考えだされたもの。

「光速度不変の原理」を採用して光速度を
「一定値c」にすると変換式が求められなくなる
相対性理論を考えるとき、必ず適用するのが光速度不変の原理。理論を導く前に必ず、古典物理学の光速度Cを誰から見ても「一定値c」に書き換えないと相対性理論の話は始まらない。これはアインシュタインから、世界中の科学者、数学者、学生、一般人、イヌもネコもみーんな同じことをしている。
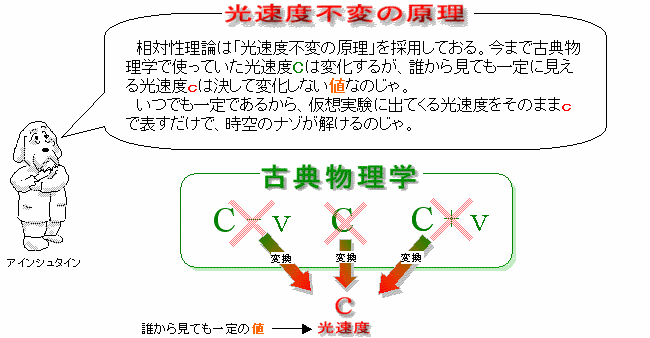
って感じでね。
ところが、数式で答を見つけるには
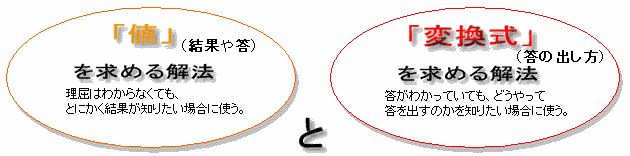
があって、「一定値c」を代入をした相対性理論は「値」を求める解法を選択しているんだ。この解法の選択が検証には引っかからないトリックとなって理論全体を崩している。
もし光速度不変の原理に従った「値」を計算したいだけなら、光速度を「一定値c」に書き換えて計算するのが当たり前で問題もないはず。だけど、相対性理論は光の速度が一定に見えるような運動方程式を求めようとしたんだから、「変換式」を見つける解法にしたがって理論を進めるべきだったんだよ。
一般的によく使う解法は、求めようとしてる関係式の代わりに未知関数を記入しておいて、わかったことから徐々に式にしてゆく解法。はじめは答ががわからなくても、変換前後の状態を比較しながら未知関数を数式に変化させるというわけ。
ところが、相対性理論の場合はというと、全部の光速度に「一定値c」を代入して、変換前の光速度をきれいさっぱり無くしてから、
と未知関数を定義している。表向きは変換式を求めているようで、実はその前に「値」を求める解法でいろいろと小細工してるんだ。
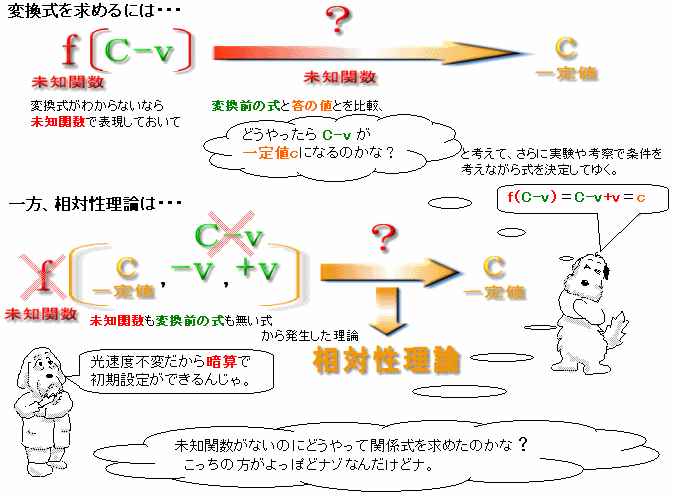
point
変換式が知りたいのなら「値」を代入するんじゃなくて、
最初から式の代わりになる「未知関数」を入れるのが正しい解法だよ。
数学の解法として、わざわざ未知関数の手がかりを消しておいて、別の未知関数を付け加えるのはおかしな操作だね。

変換式を求めたいのなら光速度不変の原理の「c」は、 「未知関数c」と考えよう
もしどうしても代入した「c」を生かして変換式を求めたいのなら、「c」を「一定値c」じゃなくて「未知関数c」として扱わないといけない。一見どうでもよさそうに思える文字の扱いは、相対性理論の評価が180度変わってしまう重要なステップなんだ。
第一、使っている文字の意味をはっきり意識しないで構築された理論が正しいかどうかの判断をすることはできないからね。きちんと理解してから先へ進める習慣をつけよう。
相対性理論の場合は「c」を「値」と決めてしまったので、最終的に運動方程式を入れる入れ物が無くなって展開がストップしちゃう。そこのところを別の新しい未知関数を付け加えて回避してる。そんなややこしいことをしなくても「c」は「未知関数c」なんだって言い切っちゃえばいい。
そうすると、はじめから変換式の入れ物「未知関数c」が用意されているので、もとの式のカタチをいじくることもなく、そのまま展開を進められる。ということは古典物理学を修正しなくても光速度不変の原理は簡単に表現する方法があったということだ。
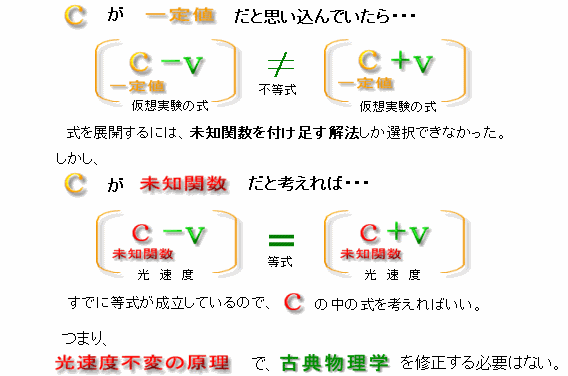
では、早速100年以上も止まっていた展開を再開させよう。
光速度不変の原理のシクミもわからないのに「c」を代入した初期の段階では、全員が未知の変換処理をしてるから、知らないうちに「未知関数c」を認めていることになるね。だから、何をどう加工して「一定値c」を算出したかは「未知関数c」を解けばわかるはず。
そしてここがおもしろいところで、「未知関数c」を解くのは光速度不変の原理の物理学的な真偽は関係ないということ。もう答を出しているんだから、みんなの記憶をたどってよーく思い出すだけでいいんだ。
point
光速度不変の原理の数式化に必要な情報は
100%頭の中から見つかるはずだよ。
光速度不変の原理には「誰から見ても」という前提条件がつきものだから、いろんな立場の観測系を想定する必要があった。そのためにわざわざ古典物理学の仮想実験で複数の座標系を想定してるわけ。「誰から見ても」の条件をクリアするにはそれしか変換理論がなかったんだ。
おそらくほとんどの人が「一定値c」を代入しただけで、ほかの変換は一切使っていないと思っているんじゃないかな。だけど、ここは数学の話。代入前に仮想実験をして、光速度を変化させていた事実をきちんと数式に取り入れなくちゃならない。
となると、光速度不変を成立させる工程は、一旦、ガリレイ変換されたC-vをまたもとの光速度Cに戻してるだけといえる。古典物理学の座標系から一歩も外へ出てないから、光速度不変の原理の変換処理はC-v+v=cだけで完結。
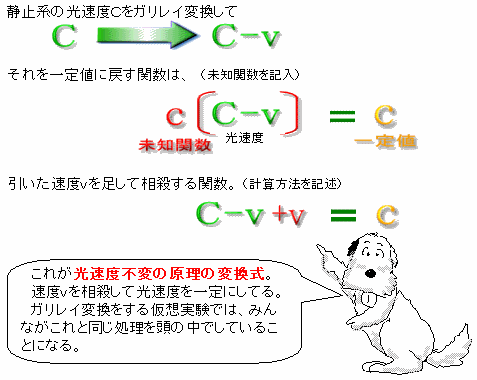
オカシナ解法でメンドウな処理をしてナンカイな理論をハツメイするより、正しい数学で正しい処理を正しく記述して、正しい解法で解いた+vの方が数学的にウツクシくない?

「c」を「一定値c」にすると始まる
相対性理論のトリックは、もう誰にも止められない
じゃあ今度は、「c」を代入した時点で「未知関数c」じゃなくて「値c」と判断した相対性理論はどんなことになちゃってるのか見てみよう。
まず矛盾なく成立していた古典物理学の式に、変換された答だけを代入したから、左辺と右辺のバランスが崩れるよね。等号でつながっていた等式が不等号でつながった不等式に変化するんだ。
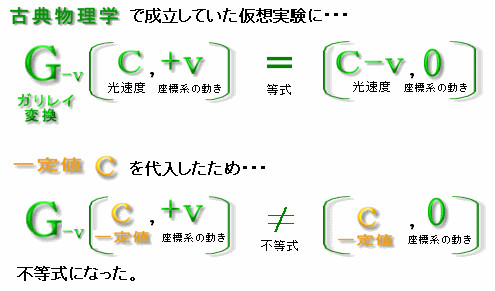
そうなると、
式が崩れたのは古典物理学が光速度不変の原理を受け入れられないからじゃ。このような誤った物理方程式は修正しなければならない。
という発想が出てくる。じゃあどこを修正する?
「c」を関数扱いにした場合は、変換された古典物理学の光速度Cだけが修正対象になってることはすぐわかるよね。ところが、「c」を「値c」にした場合は処理した痕跡を残してないから、どこを修正したらいいかわからない。式全体が修正対象になるんだ。
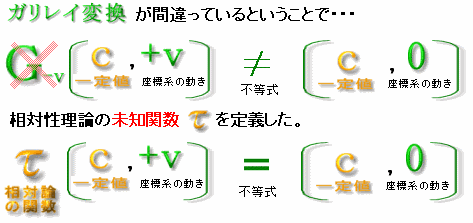
結局、まだ未知関数が無いと思い込んで、ガリレイ変換の代わりに相対性理論の未知関数τを定義する。もし、関数の知識があるなら未知関数を勝手に展開しないたりしないんだけど、未知関数と係数がマッタク同じ表記方法だということもあってトンデモない展開を可能にしてる。
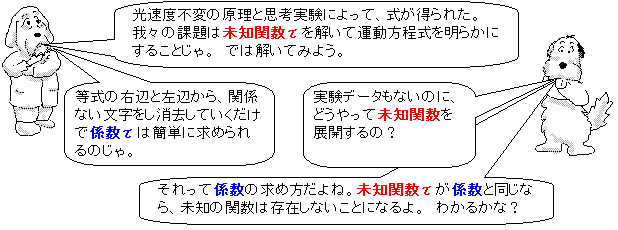
「未知関数τ」を「係数τ」と呼び変えるだけで、すんなり展開できちゃう。式のどこかに関数があるよって目印をつけただけの未知関数を加工して、関係式が解けるという考えだ。解けないから未知関数を記入していたのにね。

「係数」は関係ない時間、空間を巻き込んで
「一定値c」が崩した式を修正しはじめる
こうなったらもう本格的にトリックが活動し始めて誰にも止められなくなる。同時に大きく分けて2つの効果が現れるよ。
一つ目は関係ないものが変換式に取り込まれて、現実とはかけ離れた式ができること。観測しないで時空の理論を作るカラクリだよ。
「光速度不変の原理」で「c」を代入するときに、時間がこの位縮んで、空間がこう縮んむから「c」だ、なんて計算してないよね。変換の参考に使うのは速度だけだから、時間と空間が影響を受けないような関数を求めるために、「未知関数」を式の先頭から式の中に移動してから展開をはじめないといけない。
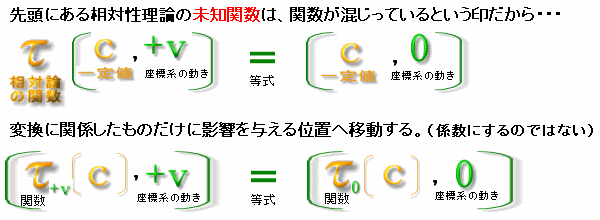
「未知関数c」を「係数c」として解いてしまった場合、移動をしないで式に使われてる中身全部、無関係な時間と空間まで取り込んで修正を加えるということになる。
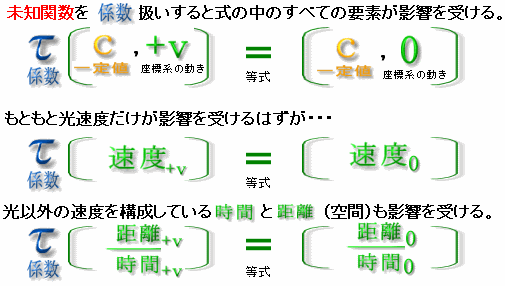
この処理では、ガリレイ変換を相殺するだけの足し算「+v」を、時間、空間、速度にまんべんなく振り分けて、時空の変換式の基礎を作ったことになるんだ。もちろん自然の法則なんかマッタク関係ないよ。

いろんな速度をvに入れるなら、
0=vが成立して相対性理論は完全に崩壊
二つ目は、あらゆる矛盾が、正しい数学で当然の結果として導かれたように見えること。関数と係数の違いも分からないで構築した理論だから、ムチャクチャな結果が出るのは目に見えてる。
相対性理論の仮想実験は古典物理学が正しいという前提からはじめたもの。後から無理やり光速度不変の原理をくっつけたから光速度は「c」に変換されてはいるけど、直前まではC-vだったんだ。この式のvはいろんな座標系で使うということで、仮の文字vで表してあるだけ、同じ速度が入るとは限らないヨ。
すると、静止系の光速度C-0を変換した変換関数「c」と、光速度C-vを変換した変換関数「c」では、式の姿カタチは同じでも数値的な処理の仕方が違っていることになるよね。だったら、光速度不変の原理の変換関数「c」を同時に2つの座標系には採用してはいけないはず。なぜかというと、同じ式の中で同じ関数「c」が、+0と+vを同時に処理できるのは、静止速度0と速度vが等しいときしかありえない。
つまり、速度0の静止系でしか光速度不変の原理は成立しない。普通の理論なら、原理の摘要範囲についても考えそうなものだけど、アインシュタインはなにも検証しないで先へ進んでる。だから、出来上がった式の速度vに0以外の数値を代入して使ってしまうんだろうね。
すると、数学の基本を崩す式が出来上がるんだ。

数学的に間違ってるから、設定しだいでいくつもの矛盾する答が出てくる。これが相対性理論の隠れた本質で、よく話題になるパラドクスの基礎にもなってるんだ。
ここまできて初期設定の間違いに気がつかなかったら、いくら立派な理論と数式を展開しても修正は無理。一番最初に値「c」を代入したのが原因だからね。
これが相対性理論のトリックの概要だよ。光速度不変の原理が出てきて、おもしろそうな物理の理論展開に気をとられていると、いつの間にか数学の基礎を無視してしまうような巧妙なシクミになってる。早い段階で「c」が未知関数だと見抜かないと、パラドックスの穴埋めのために永久に理論を増殖させ続けるようにできてるんだ。
まだまだ説明しきれないほどいっぱいシカケがあるけど、ほとんどが初歩的な算数レベルの間違いが原因だよ。
我々相対論の専門家が見つけているはずだ!」
簡単な数学の検証もできないで相対性理論を広めるシッタカ物理学者が相対論にはいっぱいいる。本当の科学者なら、
数学を無視したトリック理論を信じる前に、
人の助けになるような研究を始めているはずだよね。
それにしても、アインシュタイン先生はすごいトリックを広めてくれちゃったね。後始末が大変だよマッタク。