
勝手にメモ的解説
マイケルソン、マックスウェル、ローレンツ、ポアンカレの研究からローレンツ変換の有用性を認識していたアインシュタインは、特殊相対性理論の論文「運動している物体の電気力学について」で、完成したローレンツ変換を一旦分解し、時間軸や空間軸を変化させた理論に取り込んで、独自にローレンツ変換を導出しようと試みているが、「光速度不変の原理」の導入段階で失敗している。
これは、デカルト座標上で語られていた既存の理論をよせ集めた断片からローレンツ変換を再構築しようと考えたアインシュタインの安易な手法に原因があり、デカルト座標上のガリレイ変換の呪縛にさえ気づいていない。アインシュタインにとって、「光速度不変の原理」はデカルト座標上の各座標系で光速度cの値を一定値にすることであり、座標変換理論の根本的な見直しについて何も考察していないことからも、オリジナルの発想でないことがわかる。
アインシュタインの相対論が巧妙な数学トリックに発展してしまった根本原因を理解するには、盗用した複数の論文が古典力学的手法で表現されていたにもかかわらず、革新的な座標理論の主張に利用しようとした当然の誤謬であることを認識しておく必要があるだろう。
循環証明のための結果先取り
アインシュタインはまず最初に「光速度不変の原理」を設定した仮想実験を提示して、後からついてくる結果で自己証明をするという循環証明を用いている。もちろんこれでは何も証明できないのだが、重要なのは「光速度不変」の結果である光速度cを先に式に採用していること。
本来なら歪んだ時空理論から導かれるはずの変換式を「光速度不変の原理」の答を先に書き出すことで、時空変換式を要求されて理論展開が止まってしまうのを回避している。各座標系ともに変換の結果が一定値cで表現できてしまうのだから、既存のデカルト座標に、座標系の影響を受けない特殊な光速度cを追加しただけの理論になってしまうのは簡単に予想できる。
光速度cだけが特別扱いされる理論にもかかわらず、時空までが曲がるように設定するために、冒頭で速度の定義を導入しているが、これはデカルト座標上に限定した既存の理論で通用する定義であり、アインシュタインは独自の理論で新たに証明するべき項目となる。もし、理論の中で光速度と時空の相関関係を問われていたなら、その時点で理論が破綻してしまうため、特殊な主張が出てこない冒頭であらかじめ取り込みを完了させている。
解明するべき未知関数は存在していない
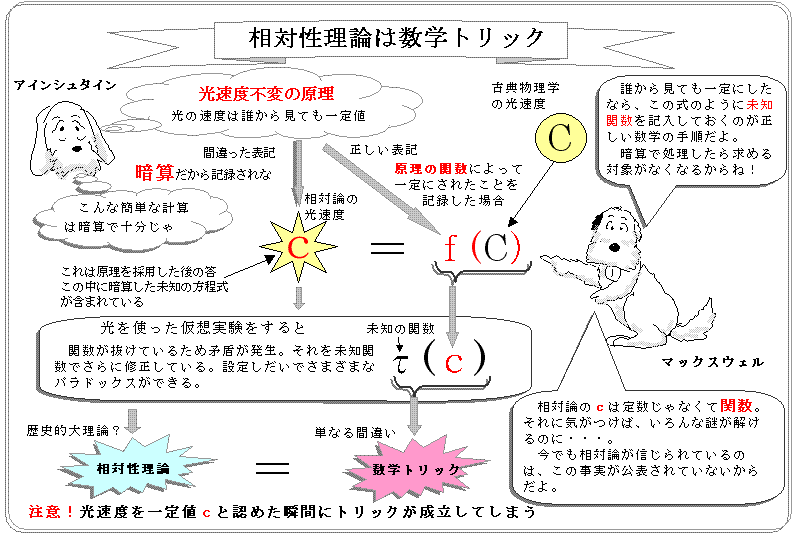
求めるべき未知数や未知関数が一定値cのみで表現されている問題文に対して、解答を期待するのは数学的に無理がある。どのように時空が変換されるかを解明するとして始めた理論に、どの座標変換にも影響を受けない一定値cを持ってこられても、展開のしようがない。
何かを求めたいのであれば、式の中に未知数や未知関数を記入して、さらにその構成を表す1つ以上の式が必要になる。例えば古典力学の光速度Cを変換する関数f(C)が記入してあれば、この関数を表現する別の式の存在から、最終的に数学的処理を解明することは可能。しかし、相対論にはアインシュタインが主張しているような時空の変換式に置き換わるような初期段階の未知関数はどこにも存在していない。
光速度「c」が未知関数扱いになる
相対論が未知の座標変換を導出した理論であるなら、はじめに座標変換を実施した「光速度不変の原理」の採用時に解明されていなかった座標変換がすでに処理さていることになる。つまり、この光速度「c」の決定方法を追求することが、アインシュタインが相対論で求めるべき未知関数の解明に他ならない。
そして「光速度不変の原理」を考察しなければ出てこない各座標系の光速度「c」は、同時に各座標系に矛盾を招いてしまう。数学上、座標変換しても一定の数値は「定数」でなく「変数」と呼ぶことになる。相対論で多発する矛盾は、数学上の「変数」を未知の変換関数が介在してもなお「定数」と定義し続けていいることに起因している。
この「定数c」を「関数c」と呼び変えるだけで矛盾を事前に解決できてしまう。理論の冒頭から採用されていることから「未知」の要素を付け加えて「未知関数c」として扱うことで相対論のナゾ解明の糸口が見えてくる。
相対論で定義されている未知関数は不要
論文「運動している物体の電気力学について」では、「光速度不変の原理」を採用した段階で光速度「c」が記入され、「未知関数c」として扱われることなく最後まで光速度「c」として、独立した扱いを受ける。もし、これが「未知関数c」だと気づいていたならば、光速度「c」を設定した状況からどのような数学的操作をしたかを数式で表すだけで解答が得られる。
アインシュタインにはそのような発想がなく、光速度「c」の影響で発生した数学的矛盾を解決するために、本来は不必要な未知関数「τ」を追加して解いている。矛盾という問題を認識したからこそ追加した「τ」だが、アインシュタインが独自に構築を進めているオリジナル理論で矛盾を感じるのもおかしなはなし。他の理論を土台にしているからこそ矛盾しているのであって、ここはアインシュタインが事前に理論の骨子を構築していれば未知関数「τ」も必要なかったはず。
「一定値c」を設定するための暗算が相対論の答
アインシュタインはデカルト座標で展開される仮想実験で、どの座標系でも当たり前のように「光速度c」を設定している。もちろんこれには「光速度不変の原理」という理由付けが必要であり、これがなければ単純にガリレイ変換で処理が進められる。
「光速度c」は「光速度不変の原理」の処理によって引き起こされた結果で、アインシュタインが独自に提唱した変換座標理論が関係式を導出するよりも前から各座標系で一定値を示すため、仮想実験のたびに実施されていたことになる。
ここで、「光速度は座標系によらず一定値c」を「一定だから一定値を記入しただけ」ではないかと考えてしまうかもしれないが、これは、相対論が完成された後の教本などで、結果のみを採用した場合にすぎない。今考えなければならないのは、アインシュタインが変換理論の構築を進めている途上で、独自の座標変換を介在させた当然の結果として一定値cを採用している事実。これを見過ごしてしまうと、相対論を検証する意味がなくなってしまう。
実際に具体的な計算を見つけるのは意外に簡単で、仮想実験の基礎となっているデカルト座標でガリレイ変換で変化する光速度をどのように処理すれば「光速度c」になるのかを考察すればいい。
例えば、静止系の光源から発せられた光をv=10万㎞/秒で遠ざかる運動系から見ると、古典力学の計算では30万㎞/秒-10万㎞/秒=20万㎞/秒になる。ただし、ここでは実験で観測された光速度を採用してはならない。いま考察しているのはデカルト座標で構成された仮想実験の座標変換についてであって、物理現象ではない。
この条件で光速度不変を成立させる目的で「光速度c」を約30万㎞/秒に修正するためには、運動系の速度10万㎞/秒の効果を相殺ればいいことがわかる。
未知関数c(v)=C+v (Cはガリレイ変換に従う古典力学の光速度)
この簡単な計算を記入せずに暗算で処理することに疑問を感じない人々が相対論を支持することになる。
理論物理学は暗算「+v」で消滅してしまう
「未知関数c(v)=C+v」を光速度「c」と表記している相対論では、仮想実験の式に矛盾が生じるが、そもそも記入されていないものを発生原因と特定できるはずがない。アインシュタインにおいては未知関数「τ」を後付けして原因を時空の歪みに押し付けてしまったことで、暗算による未知関数を探し出すチャンスを永久に失っていることになる。
現在、多くの相対論専門家と称する人々が解いているのは、論文で定義された未知関数「τ」ではなく、「光速度不変の原理」の数式化の段階で暗算で処理されたガリレイ変換の逆変換「+v」によって生じた穴を無関係な時空を歪めて埋めしているに他ならない。
言い換えれば現代の理論物理学は、特殊相対性理論をはじめとして一般相対性理論から宇宙論、ブラックホールや重力波に至るまで、仮想実験で記入されなかった「+v」が支えている。特殊相対性理論の「光速度c」は「未知関数c」の誤りであるという指摘に従って、暗算で記入されることのなかった「+v」を記入するだけで、すべてが消滅してしまう。
以上は相対論の発生要因であって、ローレンツ変換の発生についてはアインシュタインより以前の物理学者のミスに原因がある。そもそも他人の論文からローレンツ変換を再構成しようとしたアインシュタインの論文では、対象となった論文と同じミスを忠実にコピーしているにもかかわらず、導出の過程が数か所にわたり分断されているため、単独ではローレンツ変換式の導出は不可能となっている。
にもかかわらず多くの相対論の解説書で、アインシュタインの論文の不自然さや先人の論文との共通点を問題視する指摘が見受けられないのは、それだけ相対論が都合よく要約された状態で伝承されているからかもれない。100年以上前とはいえ、アインシュタインの論文を丁寧に解析すれば、まだまだトリックのナゾを解くカギはまだまだ多数見つかる。