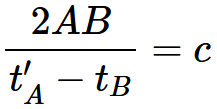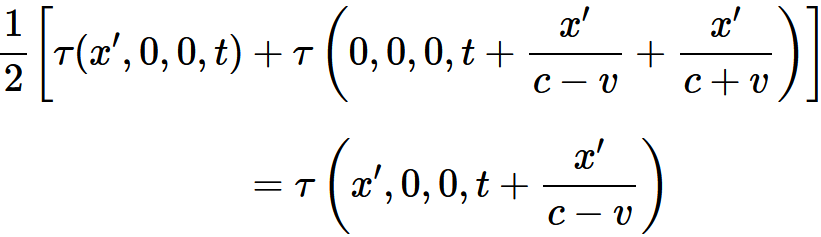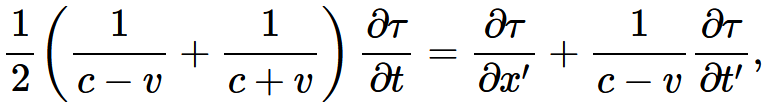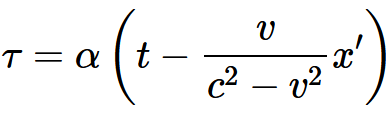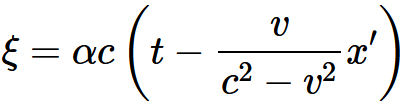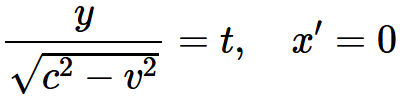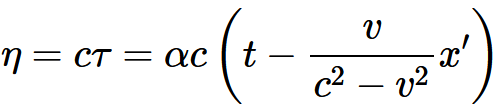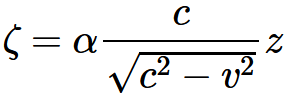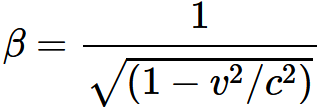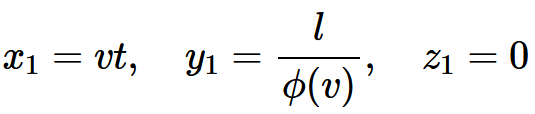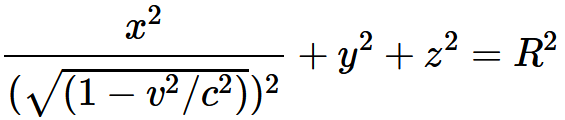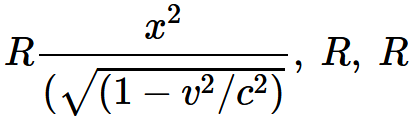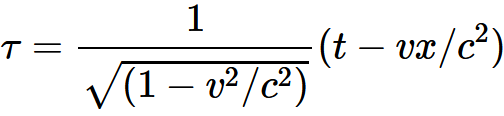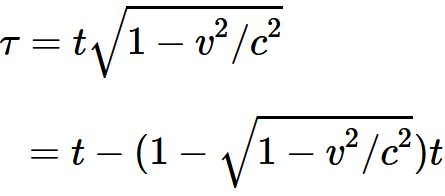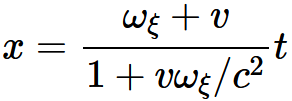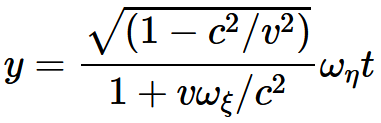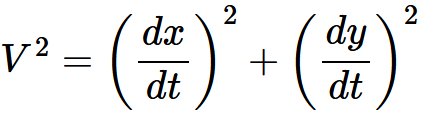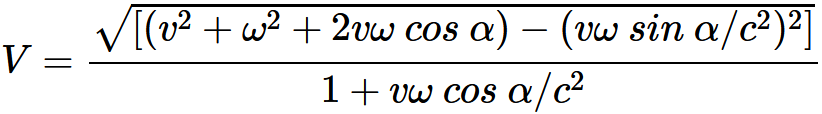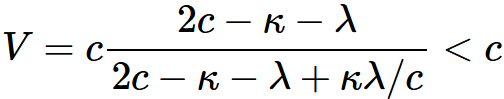「運動している物体の電気力学について」について
理論物理学をめちゃめちゃにしてしまったアインシュタインの論文は、発表当時、「難解で理解できる人が世界で数人しかいない」なんて言われてたらしい。
確かにこの論文は、いったい何を主張したくてこの手法を使っているのか全体的につかみどころのない手記のようなものになっている。論理的な流れを追いかけようとしても、急に無関係な証明が始まったりと一貫性が見えてこない。
別の言い方をすると、何人かの意見をつぎはぎしたような不自然さと、参考文献を一つも挙げていないことなど、怪しさ満載で発表当時からいろいろと話題になっている。
ここではアインシュタイン選集Ⅰの日本語訳から序文から第Ⅰ部までを取り上げて、
point
アインシュタインは何がしたかったのか?
そしてその方法は正しいのか?
という基本的な解析から、何をどうすれば正解が得られたのかを検証しようと思う。
一人でも多くこの論文を見て、相対性理論の根本的な問題に気づければいいと思う。さらにもう少し解析を進めるだけで、この論文がめちゃくちゃな構成になってしまった理由も見えてきて面白いヨ。
その詳しい解説と解析は別のページでするとして、とにかく、天才を演じていたアインシュタインの歴史的論文「運動している物体の電気力学について」の内容を見てみよう。
- 「運動している物体の電気力学について」について
Ⅰ.運動学の部
§3.座標系と時間の変換理論.一つの座標系からこれに対して
一様な併進運動をしている他の座標系への変換§4. 運動する剛体と運動する時計について得られた
方程式の物理的意味
日本語訳の誤りもそのままにしてある。まずは解説なしで読んでみてネ。

論文序文 [A1]運動している物体の電気力学について
電磁気学では光速度が一定と思われていた当時、ガリレイ変換を使う古典力学と一致しなかった原因についてアインシュタインは、
古典力学で扱う座標理論を変えてしまえば解決する。
と考えたんダ。つまり、古典力学の世界でも同じように光速度が一定になるような座標変換方法を採用すれば、光の媒体のエーテルについて悩まなくても済むと言ってる。
共立出版株式会社 アインシュタイン選集Ⅰ 訳者:中村清太郎
序文より引用, 抜粋開始[A1]運動している物体の電気力学について
Zur Elektrodynamik bewegter Körper
Ann.der Phys.17(1903),pp.891~921
現在行われている普通の解釈によると, マッスウェル(Maxwell)の電気力学は, 運動物体にあてはめた場合, 現象の種類には無関係に,対称的でない結論を導く。たとえば, 磁石と蓄電器の間に起こる交互の電気力学的作用をとるとしよう。この場合, 観測される現象は蓄電器と磁石の相互の運動だけに依存して決まる。ところが従来の考えによると, これら二つの物体のどちらかが他に対して運動している場合と, その逆の場合とで, 明確な相異があるとされていた。もし磁石が運動し, 蓄電器が静止しているときには, 磁石のまわりに一定のエネルギーをもつ電場が生じ, そのために蓄電器のある場所に電流が流れる。その反対に磁石が静止し蓄電器が運動しているときには, 磁石のまわりに電場は生じない。しかし, 蓄電器の中には最初の場合の電気力によって生じたと同じ方向の強さの電流が生じる。もちろん, この二つの場合の相対運動は等しいとする。
このような例と, さらに“光の媒質”に対する地球の相対運動を発見しようという試みの失敗とを合わせて考えると, 電気力学の現象は力学の現象と同様に, 絶対の静止という考えを立証するような性質を持っていないように見える。むしろこれらの事実から, 力学の方程式が成り立つすべての座標に対して, 電気力学や光学の法則がいつも同じ形で成り立つと考えられる*。
* このことはすでにローレンツ(Lorentz)が指摘していたが, アインシュタインはそのことは
論文を書く時には知らなかった(以下注はA.ゾンマーフェルトによる)このことは, 小さな物理量の1次の近似についてはすでに立証ずみのことである。
このような推測を第一の要請と見なして, 相対性原理と呼ぶことにする。さらに次のような第二の要請をつけ加えよう。
光は常に真空中を一定の速さcで伝播し, この速さは光源の運動状態には無関係である。
これは, ちょっと考えると, 第一の要請とは矛盾するように見えるかもしれない。しかしこれら二つの要請は, 静止物体に対するマクスウェルの理論にもとづいて, 運動物体の電気力学を簡単にかつ一貫して建設するためには十分である。いま考えている立場によると, 特別の資格をもつ絶対静止の空間の存在は必要でなく, また電磁過程の起こる真空の1点に一つの速度ベクトルを仮定しなくてもよい。このような意味で, “光のエーテル”を導入する必要はないことがわかるであろう。
これから述べる理論は, すべての電気力学と同様に剛体の運動学にもとづいている。なぜならば, この種の理論のいうところの主張は, 剛体(座標系), 時計およびいろいろの電磁過程のあいだの関係について触れるものだからである。これらの関係についての考察が従来不十分であったということが, 現在の運動体の電気力学に内在する困難の原因なのである。
序文引用終り

Ⅰ.運動学の部 §1.同時性の定義
今までの常識では、だれにとっても時間の進み方は同じと思われていたが、それを根本から見直すための準備として、1つの座標系を「定常系」と定義して時間の測定方法を規定している。
引用, 抜粋開始Ⅰ.運動学の部
§1.同時性の定義
いまニュートンの力学の方程式がよい近似で成り立つような一つの座標系を考える。表現を適確にし, かつこのような座標系をあとで導入する他の座標系とことばのうえではっきり区別するために, この座標系を定常系とよぶことにしよう。
もし質点がこの座標系について静止しているなら, その位置は, 測定用の固定した標準と, ユークリッド幾何学の方法とを用いることによって, その座標系に関連して定義することができる。そして, その位置は直行座標系によって表すことができる。
質点の運動を記述する場合には, その座標の値は時間の関数として与えられる。ここで一つ注意すべきことがある。それはこのような数学上の記述は, “時間”をどのように考えるかを明確にしないかぎり, 物理的には無意味だということである。時間が関係するわれわれのすべての判断は, 常に同時に起こる事件についての判断なのである。たとえば, 私が
「あの汽車はここに7時に到着する」
というとき, それは
「私の時計が7時を指すことと, あの汽車の到着とは, 同時に起こる事件である*」
という意味なのである。
* ここでは近似的に同じ二つの場所における二つの事件の同時性という概念のもつ不正確さには立ち入らないことにする。この不正確さは, 単に抽象的にはとり除くことはできても, 実際には取り除くことはできないものである。
“時間”の定義についてのすべての困難さは, “時間”の代りに, それを“私の時計の針の位置”によっておきかえれば解決できると思われるかもしれない。事実, このような定義は, 時計のある場所だけについては正しい。しかし離れた二つの場所で起こる別の時間の二つの事件を関連させようとするときには正しくないのである。つまり, 上記の定義は違った場所でつぎつぎと違った時間に起こる一連の事件を関連させようとするときにはもはや正しくない。あるいはこれと同じ結論になるが, その時計から離れたいくつかの場所で起こるいくつかの事件の時間を測ろうとするときには上記の定義は成り立たないのである。
もちろん, 座標の原点に時計をもった一人の観測者がいて, 測ることになっている各事件の時間を定める時計の針の位置を光の信号によって連絡し, その信号がその観測者に真空を通って到着する, というように配置すれば, そのようにして決まる時間の値で満足するべきであるかもしれない。しかしこのような連絡の方法は, 経験的に知られているように, 時計をもっている実際の観測者の立場に無関係ではないという点で不利である。以下では, この線に沿ってもっと実際的な時間の測定法を考えることにしよう。
いま, A点に一つの時計があるとする。A点にいる観測者は, Aのごく近くに起こる事件の時間の値を, これらの事件と同時である時計の針の位置を測ることによって決定することができる。また空間のB点に, A点にある時計とすべての性質が等しい時計がもう一つあるとするとき, B点にいる観測者は, B点のごく近くで起こる事件の時間を測定することはできる。しかし, 時間を比較するためにそれ以上の仮定をしないかぎり, A点での事件とB点での事件とを比べることはできない。われわれはこれまでの議論では, “A点での時間”と“B点での時間”を定義しただけである。しかし, われわれはAとBとに共通の時間は定義していなかった。なぜなら, AからBへ光が進むために必要な“時間”とBからAに光が進むために必要な“時間”とが等しいということを定 義によって確立しないかぎり, この共通の時間はまったく定義できないからである。いま光が“A時間”のtA にA点を出発してB点に向かって進み, “B時間”のtBにB点で反射してA点にもどり, 再び“A時間”のt'A にAに着いたとする。定義により, もし
・・・・式 1-1が成り立つならば, この二つの時計は同調していることになる。いま, このような同調の定義には矛盾はなく, 二つ以上の多くの点についても定義ができて, かつ次の二つの関係が常に成り立つと仮定しよう。
1.もしB点の時計がA点の時計と同調すれば, A点の時計はB点の時計と同調する。
2.もしA点の時計がB点の時計と同調し, かつC点の時計とも同調するなら, B点の時計とC点の時計もお互いに同調する。
このようにして, 思考物理実験の助けによって違った場所にある定常的な時計の同調ということの意味を定め, “同時性”とか “同調”とか“時間”とかということばの定義を明確に定めた。一つの事件の“時間”とは, その事件の起こった場所にある定常的な時計によって, その事件と同時として決まる時間である。もちろん, この時計は特別の定常的な時計と同調的であり, したがってまた, すべての時間の測定に対して同調しているとする。
さらに経験的事実に従って,
・・・・式 1-2という量は, 普遍定数――真空中の光速度――であると仮定しよう。
定常系における定常時計によって時間を測定するということは本質的なことである。このようにして定義した時間は定常系に固有なものであるから, “定常系における時間”とよぶことにしよう。
§1.同時性の定義 引用終り

§2.長さと時間の相対性
相対性原理と光速度不変の原理を両立させると、 もはや同時という概念は絶対ではなくなるのじゃ。
ということを仮想実験と式で説明している。
引用, 抜粋開始§2.長さと時間の相対性
これから述べる意見は, 相対性原理と光速度不変の原理にもとづいている。これら二つの原理を次のように定義しよう。
1.物理系の状態の変化を記述する法則は, その状態の変化を, お互いに等速運動をしている二つの座標系のどちらについて記述してもその形は同じである。
2.光は座標の“定常”系をいつも一定の速さcで伝わる。この光が定常の物体または運動物体から発しても同じである。したがって
・・・・式 2-1ここで時間の間隔とは§1 の定義に従って決めたものとする。
いま, ここに定常の剛体の棒があるとする。そしてこの定常的な測定棒によって, その長さ ℓ を測ったとする。さらに, この棒の軸は一つの定常系のχ軸 に沿っていて, χの増加する方向に χ軸に沿って平行移動させたものとしよ う。さて, この動いている棒の長さを調べてみよう。その長さは次の二つの手順によって確かめるべきものとする:
(a) 観測者と測定用の棒, および測定の対象となる棒とはいっしょに運動し, 観測者は測定用の棒を, 測定されるべき棒に直接当てることによって後者の長さを測定する。この三者の関係はお互いが静止しているときと同じである。
(b) 定常系にとり付けた定常時計を§1 の考えに従って同調させておく。観測者はある一定の時間に, 測定されるべき棒の両端が定常系のどの点に存在しているかをこの時計によって確かめる。いま使用した測定棒(この場合, 静止している)によって測った, これら2点間の距離は“棒の長さ”と認定することのできる長さである。相対性原理によれば, (a)の操作によって決まる長さ(これを運動系における棒の長さとよぶ)は定常棒の長さ ℓ に等しいはずである。
(b)の操作によって決まる長さは, 定常系における運動している棒の長さとよぶべき長さである。このことから, この長さを上記の二つの原理にもとづいて決めてみよう。その結果は ℓ とは違ったものになるであろう。
従来の運動学によると, これら二つの操作によって測った長さは正確に等しいということを, よく考えないで仮定している。換言すれば, 運動している棒はtという時間には幾何学的には一定の位置に静止している同じ物体によって完全に表わされていると仮定している。
さらに棒の両端Aと Bに, それぞれ定常系の時計と同期させた時計を置くと しよう。つまり, それらの時計の指す結果は各瞬間においてその場所での“定常系の時間”に対応する。したがって, それらの時計は“定常系に同期”しているものである。
さらに, おのおのの時計の場所に運動している観測者がいて, 彼らは§1 に定めた規準によって二つの時計を同調したものとする。
光がA点から時刻tA に出発し, tB にB点で反射して, 時刻t'A に再びAに もどったとしよう。光速度不変の原理を考察すると,
・・・・式 2-2および
・・・・式 2-3となる。ここでrAB は定常系で測った運動している棒の長さである。したがって, 運動している棒とともに運動する観測者は二つの時計は同調していなかったというであろうが, 定常系の観測者は二つの時計は同調していたと主張するであろう。
このようにして, 同時性という概念には, 絶対的な意味をもたすことはできないことがわかるであろう。二つの事件が一つの座標系から見て同時刻に起こったように見えても, その座標に対して運動している別の座標から見ると, もはや同時刻の事件と見ることはできなくなるのである。
§2.長さと時間の相対性 引用終り

§3.座標系と時間の変換理論.一つの座標系からこれに対
して一様な併進運動をしている他の座標系への変換
ここはローレンツ変換係数を導出している相対論の心臓部ともよべるところ。にもかかわらず、アインシュタインが数学の基本を理解できていなかったことがよくわかって興味深いヨ。
引用, 抜粋開始§3.座標系と時間の変換理論.一つの座標系からこれに対
して一様な併進運動をしている他の座標系への変換“定常的”な空間に二つの座標系をとる。これらは1点から出る三つのお互いに垂直な剛体の直線から成る二つの系とする。この二つの座標系のX軸が重なっていて, Y軸とZ軸はそれぞれ平行であるとする。また, おのおの系に は測定用の剛体の棒と数個の時計とがあり, これらの二つの測定用の棒と二つの系にあるすべての時計は, すべての性質が同じであるとする。
さて, この二つの系のうちの一つ(k系)の原点が, 他の定常系(K系)のχの増す方向に一定の速度vで運動するものとしよう。座標系の各軸や使用する測定棒および時計も同じ速度vで運動するものとする。そうすると, 定常系の各時刻ごとに運動系の各軸の位置が決まるであろう。そして対称性の原理によって, k系の運動は時間において定常系の軸に平行にとることができると仮定しよう(この“t”はいつも定常系の時間を表わす)。
さて, 定常系Kから定常な測定棒によって測られる空間を考える。この空間はまた, 運動系kからは運動系とともに動く測定棒によって測るものとする。このような測定によって, 座標χ,y,z およびξ,η,ζが得られる。さらに定常系の時間tは, 時計の存在するすべての場所に対して, §1に述べたような光の信号の方法によって測られるものとしよう。同様に運動系の時間τは, その系について静止している時計の置かれているすべての運動系の点に対して, §1で述べたように, このような時計の置かれている各点間に光の信号の方法を用いることによって測られるものとしよう。
定常系Kで起こる一つの事件の場所と時間を完全に定義する値の組χ, y, z, t に対して, 運動系kについて同じ事件を定義する値の組ξ, η, ζ, τが対応する。われわれの課題は, これらの量の関係をつける方程式の組を見いだすことである。
第一にこれらの方程式は1次でなければならない。なぜならば, 空間と時間は斉一という性質をもつと仮定したからである。もし
・・・・式 3-1とおくと, k系に静止している1点は時間に無関係なχ',y,z という値の組を持つはずである。まずτをχ',y,zの関数として定義する。そのためには, τは運動系kに静止している時計の得た知識の総合にほかならないということを方程式で表わさねばならない。この時計はもちろん§1で述べたような規則によって同調させてあるものとする。
運動系kの原点から一つの光線が時間τ0 にX軸に沿って, χ' まで放射されたものとする。そして時間τ1 にそこで反射されて座標系の原点に向かい, 時間τ2 に原点に着いたとしよう。その場合
・・・・式 3-2を得る。あるいは定常系に対して, 関数τについての上の議論と光速度不変の原理を当てはめることによって, 次の関係を得る:
したがって, もしχ′を無限小の値にとると,
・・・・式 3-3あるいは
・・・・式 3-4・・・・式 3-5となる。
ここで注意すべきことは, 座標の原点の代りに光線の原点として他のどのような点をとることもでき, その場合に得られる方程式は, したがってχ',y,zのすべての値に対して成り立つことである。
同じ議論をY軸およびZ軸について当てはめると
・・・・式 3-6を得る。ただし定常系から見ると, 光は常にこれらの軸に沿って速度
で伝播するということを考慮しなければならない。
・・・・式 3-7さてτは1次の関数であるから, これらの方程式から次の式が得られる:
ここでαは, いまのところ未知関数φ(v)であり, 簡単のために, t=0のと きk系の原点においてτ=0と仮定しよう。
このような結果を用いると, 光は運動系において測っても速度cで伝播するということを方程式で表わすことによって, 容易にξ,η,ζという量を決定することができる。(このことは, 相対性原理による光速度不変の原理の要求に従うものである)。ξの増加する方向に時間τ=0で放出された光線に対して
・・・・式 3-8または
・・・・式 3-9が成り立つ。しかし, この光線は定常系で測ると, k系の出発点に対して, 速度c-vで動いている。その結果
・・・・式 3-10を得る。
もし, このtの値をξに対する方程式に代入すると
・・・・式 3-11を得る。同じようにして, 光線が他の二つの軸に沿って運動する場合に, もし
・・・・式 3-12,3-13ならば
・・・・式 3-14が成り立つ。
したがって
・・・・式 3-15・・・・式 3-16を得る。χ′に対してその値をおきかえると
・・・・式 3-17_t・・・・式 3-17_x・・・・式 3-17_y・・・・式 3-17_zここで
・・・・式 3-18であり, φは, いまのところvの未知の関数である。もし運動系の最初の位置とτの原点について何か特別の仮定をしないかぎり, 加算的な定数をこれらの方程式の各右辺に付け加えておくべきである。
さて運動系から見て, どのような光線も速度cで伝播するということを証明しなければならない。もちろん, すでに示したように, 定常系では光速度がcだということを前提とした場合のことである。なぜならば, われわれはまだ光速度の不変性の原理が相対性原理と両立するということの証明を行っていないからである。
定常系と運動系が共有するとき,
・・・・式 3-19において原点から球面波が放出されて, K系において速度cで伝播するものとしよう。この波に付着した1点を(χ,y,z)とすると
・・・・式 3-20が成り立つ。
この方程式を, 先に示した変換の方程式の助けをかりて変換すると, 簡単な計算の結果
・・・・式 3-21を得る。したがって, この波は運動系から見ても光速度cで伝播する球面波となる。この結果, われわれの二つの根本原理は両立することがわかる*。
* ローレンツ変換の関係式は, それを使って
という関係式から第二の関係式
が当然の結果として導かれるべきであるという条件を課すことによって簡単に導くことができる。
ここで使った変換の方程式のなかにはvの未知関数φが含まれているので, 次にその形を決めることにしよう。
この目的のため第三の座標系K' をとり, K' 系はk系に対してはX軸に
平行に運動し, 運動系k系の座標原点がX軸上で-vの速度で動くようにとることにする。時間t=0でこれらの三つの系の原点は一致し,
・・・・式 3-22のとき, K’系の時間t' はゼロとする。K' 系で測った座標をχ',y',z' とし, 上述の変換の方程式を2回使うことによって次の関係式を得る。
・・式 3-23_t・・式 3-23_x・・式 3-23_y・・式 3-23_zχ',y',z' とχ,y,z の間の関係は時間を含まないから, K系はK' 系はお互いに静止しており, かつ, K' 系からk系への変換は恒等変換になるはずだということは明らかである。したがって
・・・・式 3-24となる。
さて, φ(v)の意味を調べてみよう。k系のY軸において
・・・・式 3-25と
・・・・式 3-26のあいだにある部分を注目してみよう。Y軸のこの部分は, K系に対しては, その軸に垂直に速度vで動いている一つの棒に見える。K系においては, その両端は次の座標で表される。
・・・・式 3-27および
・・・・式 3-28したがって, K系で測ったこの棒の長さはl/φ(v)である。これによって関数 φ(v)の意味が明らかになる。対称性の原理により, 定常系から測ったときその軸に垂直に働く棒の長さは速度だけに依存し, 運動の方向と向きとには無関係のはずである。したがって, 運動している棒の長さを定常系で測るとき, vを-vにおきかえてもその長さは変わらない。そこで
・・・・式 3-29あるいは
・・・・式 3-30を得る。この関係式と, すでに示した関係式とから
・・・・式 3-31が得られ, その結果, すでに見つけた変換の方程式は次の形をとる。
・・・・式 3-32_t・・・・式 3-32_x・・・・式 3-32_y・・・・式 3-32_zここで
・・・・式 3-33である。
§3.座標系と時間の変換理論 引用終り
§4. 運動する剛体と運動する時計について得られた
方程式の物理的意味時間と空間が、ローレンツ変換によって変換されて伸縮するという主張。
引用, 抜粋開始§4. 運動する剛体と運動する時計について得られた
方程式の物理的意味運動系kと静止していて中心がk系の原点にあるような一つの剛体球*(半径R)をとる。* これは静止しているときに測ったときに球体をしているという意味である。
この球が速度vでK系に対して運動しているとすると, その表面の方程式は
・・・・式 4-1で与えられる。時間t=0 において, この表面の方程式を χ,y,zで表すと,
・・・・式 4-2となる。したがって, 静止しているときに測って剛体球の形をしていたものは, 運動しているときには静止系から見て回転楕円体の形を示す。その三つの軸は
・・・・式 4-3で与えられる。
したがって, その球(そして球だけでなく, どのような形をした剛体についても) のY方向とZ方向の大きさは運動によって変化を受けないが, X方向の 大きさは
の比で小さくなって見える。換言すれば, 速度の値v が大きいほどその短縮の程度も大きくなる。v=c のとき――“定常系”から見て――すべての運動物体は平面の形に縮んでしまう。また光速度より大きな速度に対しては, 我々の推察は無意味となる。しかしあとで示すように, われわれの理論では光速度は物理的には無限に大きな速度の役割を果たすのである。
同じような結果は, “定常”系に静止した物体を一様な運動をしている系から見たときにも成り立つことは明らかである。
さらに一つの時計があって, 定常系に対して静止しているときに時間tを記録し, 運動系に静止している時に時間τを記録するようになっていたとし, この時計をk系の座標原点に置いてちょうど時間τを記録するように調整したものとしよう。定常系から見たとき, この時計の速さはどうなるであろうか。
時計の位置について決まる量χ,t およびτの間には, 明らかに
・・・・式 4-4の関係が成り立ち, かつ
・・・・式 4-5である。したがって
・・・・式 4-6となる。そこで(定常系から見て)時計の記録する時間は1秒間に
だけ遅れる。あるいは第4次およびそれより高次の量を無視すると,
だけ遅れる。
このことから次のような奇妙な結果が導かれる。もしK系の2点AとBとに それぞれの定常時計があって, 定常系から見て同調しているものとする。いまAの時計が直線ABに沿ってBのほうへ速度vで運動するとすると, これがBに 着いたときには二つの時計はもはや同調していない。AからBへ運動した時計は, Bに止まっていたもう一つの時計よりも
だけ(第4次およびそ れより高次の量を無視)遅れている。ここでtはAからBへの旅行に要する時間である。
すぐわかるように, この結果は, 時計がAからBへとどのように折れ曲がった多角形の道を通って行ったときにも成り立つし, また点AとBが一致しているときにも成り立つ。
もし多角形の道について証明した結果が, また連続的カーブした道についても成り立つとすれば, 次のような結果が得られる:
A点にある二つの同調した時計の一つが等速度で一つの閉じた曲線上を運動して再びAにもどったとし, その運動に要した時間をtとすると, その運動に参加した時計がAに着いたとき, Aに静止していた時計から見て
だけ遅れていることがわかるであろう。したがって, 赤道に置かれた時計*は 両極どちらかに置かれた, まったく同じ性質の時計に比べて, 他の条件が全部同じといて, ごく僅かだけ遅れるはずである。
*地球が属している物理系ともいうべき振子時計ではない。この場合は除外すべきである。
§4.運動する剛体と運動する時計について得られた方程式の物理的意味 引用終り
§5.速度の合成
ここまでの結果をまとめて、
速度の合成則も書き換えることによって
光速度不変の原理が成立するのじゃ。という主張。
引用, 抜粋開始§5.速度の合成
K系のX軸に沿って速度vで動いている系kにおいて, 一つの点が方程式
・・・・式 5-1・・・・式 5-2・・・・式 5-3に従って運動したとする。ここでwξとwη は定数である。
この点の座標系における運動に対する要請
その点の従う運動方程式のなかへ, §3 の平行移動の方程式を利用して, χ,y,z,t という量を導入すると
・・・・式 5-4・・・・式 5-5・・・・式 5-6を得る。したがって, 我々の理論では, 速度の平行性の法則は第一近似としてしか扱えない。ここで
・・・・式 5-7・・・・式 5-8・・・・式 5-9とおく。αはこのばあは二つの速度vとwのあいだの角度と見るべき量である。簡単な計算によって, 次の関係式が得られる。
・・・式 5-10vとwとの役割はその合成速度の式の中で対象的になっている。これは注目すべきことである。もしvもまたX方向を指していたとすると,
・・・・式 5-11を得る。この方程式から, c以下の二つの速度を合成してもc以下の値しか得られないという結論が導かれる。なぜならば, もし
・・・・式 5-12とおくと, k, λは正でc以下であるから
・・・・式 5-13となるからである。
さらに光速度cと光速度以下の速度を合成しても, その結果は光速度に等しい。この場合には
・・・・式 5-14だからである。
またvとwが同じ方向を向いている場合, §3 の議論により, 二つの変換を続けて行うことによりVに対する式が得られる。もしKとkの座標系のほかに, §3 で示したようなk系に対して平行に動くもう一つの座標系k’を導入すると χ,y,z,tという量とk’系におけるこれに相当する量とのあいだの方程式が導かれる。k’系における量は§3 で導いた方程式において, vの代りに
・・・・式 5-15をおきかえると得られる。この事実から以上のような平行移動は必然的に群をつくるということがわかる。
以上われわれの二つの原理に対する運動力学の理論の要請的法則を示したが, 次には電気学に対するその応用例を導くことにしよう。
§5.速度の合成 引用終り
理解できたら心配
どうだったかな? すごくよく理解できた? これを何の問題もなく理解して解説している学者もいるらしいけど、別のページの解説で指摘していることに正解を見つけられないようじゃ数学も物理もやめたほうがいいヨ。
理解できないなら、もっとわかりやすくした解説からその理由を見つけてみよう。
ただし、まだ作成中。