マイケルソン・モーレーの検証式を反射の法則の適用のし方に着目すると
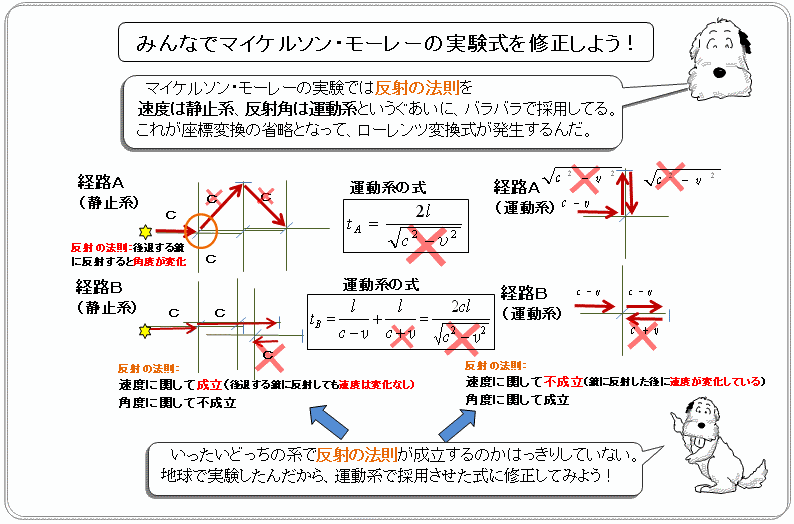
マイケルソン・モーレーの検証式を反射の法則の適用のし方に着目すると
静 止 系 運 動 系(地球上の実験装置)
反射角 速度 反射角 速度 経路A 不成立 成立 成立 不成立
経路B 不成立 成立 成立 不成立
反射角 速度 反射角 速度 経路A 不成立 成立 成立 不成立
経路B 不成立 成立 成立 不成立
といった具合に、運動系では速度について反射の法則が成立していない。
これでは、未発見の性質を持った光を想定したも同じ。地球上で実験したんだから、運動系で反射の法則が成立するように検証式を修正してあげないとね。
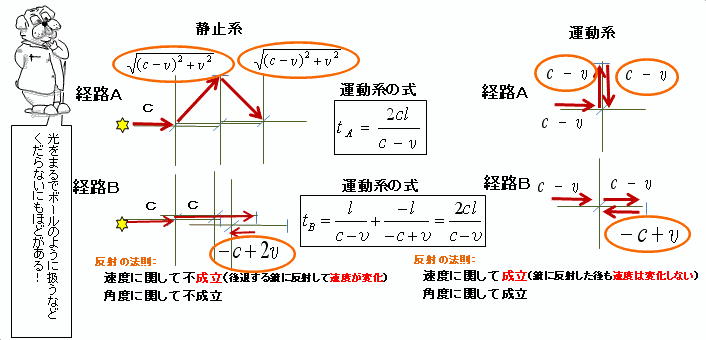
(簡単のためにℓの長さをc-vに設定すると計算しやすいよ。)
つまり、はじめから
マイケルソン・モーレーの検証式は間違っていた
古典物理学を正しく表現した式じゃなかったんだ。
運動系と同じ反射の法則を静止系で適用したことで、座標変換関数が見落され、その結果、ローレンツ変換式が発生する。その分だけ逆にローレンツ変換して戻したのが相対論だよ。こんなメンドーなことしないで、はじめから普段観測されているように反射の法則を適用させていれば、相対論の反証実験だったことに気付く学者も現れるかもネ。
 「光をまるでボールのように扱うなんて、くだらないにもほどがある!
「光をまるでボールのように扱うなんて、くだらないにもほどがある!
マイケルソン・モーレーの実験で干渉縞が観測されなかったことから、
修正係数を求めると相対論のローレンツ変換が得られるのだ!」
こんな感じでミラーに反射した後の光が、ボールのように変化することに文句つけてる専門家がいるけど、マイケルソン・モーレーの検証式が光をボールのように扱っていることも理解できてなかったなんて、物理学の夜明けはまだまだ先ダネ。
なぜ、反射の法則を分解してバラバラに適用しているのか?
これくらいは説明してくれないと、生徒の相対論離れは止まらないよ。