Ｅ＝Ｍc^２は架空の式

１９４６年に発表された「質量とエネルギーの初等的証明」では、質量からエネルギーへの変換にc^２の係数が関係してると分かって、みんな相当びっくりしたみたい。何しろリンゴ１個が大きな山を吹っ飛とばすくらいのエネルギーを持ってるらしい。安っぽいＳＦではよくこの式が出てくる。それほどみんなにスゴイ式だと思われてる証拠だね。

この式は相対論と同じようなトリックを使って創作されてる。「質量とエネルギーの初等的証明」ではＥ=Ｍc^２の簡単な導出法を説明（証明？）してるから、注意深く読めば必ずトリックも見つかるはずだよ。

質量とエネルギーの等価性の初等的証明
Albert Einstein.Elementary derivation of the equivalence of mass and energy
Technical Jornal, vol, 5(1946,) pp.16〜17

この理論は一般相対論の原理と、次の三つの法則を用いたものである。

１.運動量保存の法則

２.輻射圧の式、すなわち一定方向に進む輻射の複合体の運動量

３.よく知られた光行差の式（恒星の見かけの位置に対する地球の運動の影響―ブラドレー）

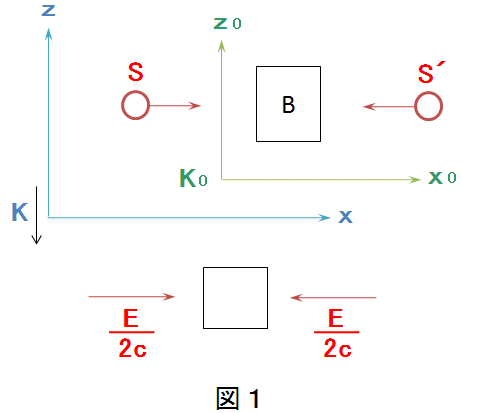
いま、物体Ｂが座標系Ｋに対して空間に力を受けずに静止しているとする。二つの輻射複合体Ｓ、Ｓ´がれぞれＥ/２のエネルギーをもって正負のｘ０方向に進み、Ｂに吸収されＢのエネルギーがＥだけ増加した。対称性の理由から物体ＢはＫ０に対して静止を続ける。

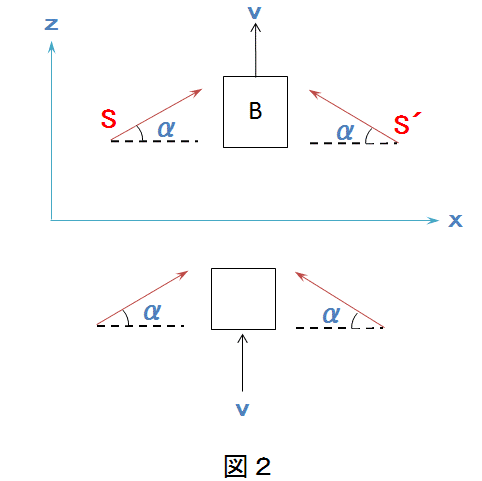
さて、同じ過程をＫ０に対して一定の速度ｖで負のＺ０方向に動いている座標系Ｋから眺めたとしよう（図１）。その場合、Ｋに関しては上の過程の記述は次のようになる。

物体Ｂは正のｚ方向に速度ｖで動き、二つの輻射複合体Ｓ、Ｓ´はＫのｘ軸に対して角αをなす方向を持っている（図２）。光行差の法則によれば、第１近似でα＝ｖ/ｃ（ただしｃは光速度）である。Ｋ０における考察から、Ｂの速度はＳおよびＳ´の吸収のあとで変わらないことがわかる。

座標系Ｋにｚ方向の運動量保存則をこの系に適用してみよう。

１．　吸収前のＢの質量をＭとすれば、ＭｖはＢの運動量を表わす。(古典力学によれば)、おのおのの輻射複合体はＥ/ｃのエネルギー、したがってマックスウェル理論のよく知られた結果からＥ/２ｃの運動量を持っている。これはＳのＫ０系に関する運動量である。

しかし、ｖがｃに比べて小さければ、Ｋに関する運動量も２次の微小量（１に対してｖ^２/ｃ^２）を無視すれば同一である。運動量のｚ成分は（Ｅ/２ｃ）sinα　あるいは十分な正確さで（高次の量を無視して）（Ｅ/２ｃ）α＝（Ｅ/２ｃ）（ｖ/ｃ）である。したがって、Ｓ、とＳ´とを合わせてＥｖ/ｃ^２の運動量をｚ方向に持っている。したがって吸収前における系の全運動量は、Ｍｖ＋（Ｅ/ｃ^２）ｖとなる。

２．吸収ののちのＢの質量をＭ´とする。ここでエネルギーＥを吸収したために質量が増加したことが予言される（これは考察の最後の結果に矛盾が生じないために必要である）。したがって吸収ののちの運動量は、

Ｍ´ｖ

である。

さて、運動量保存則をｚ方向に対して適用すれば

Ｍｖ+（Ｅ/ｃ^２）ｖ＝Ｍ´ｖ

すなわち

Ｍ´−Ｍ＝Ｅ/ｃ^２

この式はエネルギーと質量の等価性を表す。エネルギーの増加Ｅに対して質量の増加Ｅ/ｃ^２が伴う。通常の定義によれば、エネルギーは付加定数だけ未定のままであるから

Ｅ=Ｍc^２

になるようにこれを選ぶことができる。

この論文は途中で同じ文字を違った意味に再定義したり、しなくてもいいような不自然な設定変更をしている箇所がいくつもあるから、惑わされないように注意点をあげておこう。

• 二つの輻射複合体Ｓ、Ｓ´のエネルギーをＥからＥ/ｃに再定義
• 輻射複合体のｚ成分sinαを近似値ｖ/ｃに置き換え
• ｖ^２/ｃ^２を２次の微小量として無視
• 仮想実験が終わった後で、作式
• 質量を速度ｖで運動させた後ｖで割る
• エネルギーのｚ成分をｖ/ｃで取り出す
• 質物体Ｂの質量ＭがＭ´に増加したものをＭと再定義

上のようなことをするとどうなるか。アインシュタインは気づいていたのかいないのか？　式を簡単にするのが目的なら、最初からそのように設定できたはず。あとから処理するというというのは、トリックを発生させてしまうので避けた方がよかったんだけどね。

もし、関係のわかっていない質量ＭとエネルギーＥをいきなり等号で結んで、

なんて大声で発表しても、だれもびっくりしないよね。
「質量とエネルギーの関係をイコールでつないだだけで、何も証明してないじゃないか！」
なんてツッコミが入るに決まってる。アインシュタインも同じことを考えたのかな。論文の中で、 と言いきっちゃったから、この直後にエネルギーＥが物体Ｂの質量増加分に変換されたと仮定したことを表わす式、 が書けたはず。ついでに、Ｍ´−ＭからＭへの再定義もここで実行できるから、 なんて最高にシンプルな式の出来上がり。

ちょっとまてよ。ここでこんなストレートな式を出してしまったら誰も相手にしてくれない。そりゃそうだよね。誰が見たって、
「最初の仮定を式にしただけじゃん。それに変換係数がないから全然説得力に欠けてる」

じゃあどうすればいい？

とりあえず、ひたすら仮想実験と再定義をして関係ない文字をゴチャゴチャ詰め込むってのはどう。たとえば、同じ現象を別の運動する座標系から眺めたり、ｚ成分だけ取り出したり、文字の定義を変えたり、とにかく「質量ＭとエネルギーＥの等価は仮定です」ってことが一目で分らないようにする。そしたら、おもむろに式を表に出すんだ。さりげなくホイッとネ。

すると不思議なことに、元になった式が仮定でも、受ける印象は全然違う。

「同じ現象を座標系を変えて考察するとはなんとユニークな。高度な理論物理学のテクニックを拝見させてもらおう」

大勢のギャラリーに囲まれても堂々と、

「オオ−！　なんと美しい式だ！！　これこそ究極の真理だ！！！ さすが天才アインシュタイン先生！！！！」

ヘェー、そんなにビックリマークつけるほど、すごい方法だったんだね。そうだと思ってたよ。みんなも同じ方法でいろいろ証明してみよう。って、まだ証明終わってないよ、オイオイ！

最初の仮定式にc^２をくっつけただけだよね！これ！！

「それが莫大な数字になるからもっとスゴイのだ！　ああ！！　偉大なアインシュタイン先生！！！！！」

あの！　その！！　莫大な数字を求める手順をふんでなかったんだけどぉ−ッ！！！！！！

「それが何か？！！！！　アインシュタイン先生−−−−ッ！！！！」

じゃあもっと美しくしようよ！　ＭとＥの変換係数以外にc^２が付け足された状態では、c^２は付加定数だけ未定のままであるから、ホイッ！

になるようにこれを選ぶことができる。

振りだしに戻しといてあげたヨぉ−ッ！　アインシュタイン先生−ッ！！！

ってこと証明してくれてアリガト−−−−！！！

輻射複合体も物体Ｂも座標系もＭ＝Ｅを隠すためのカモフラージュ。それにｃはもっといらない。とにかく天才物理学者もダマだまされる仕掛けがいっぱい詰まったＥ=Ｍc^２の謎解きは始まったばかりだよぉ−−−−ッ！！！！　アインシュタイン先生−−−−−ッ！！！！！

歴史的な論文がこんなに短いなんて。書いてあることが正しいなら簡潔な論文の方がいいよね。この短さは逆に誤解を招くことにもなってる。アインシュタインはこの論文で何を証明しようとしたんだろう。予想になってしまうけど・・・、

って言いたかったのかな？

c^２という係数を求めてるからには当然、数量を扱えるように数式で理論を展開する必要がある。でも論文には理論式しか出てこない。どんなに展開しても量を扱えるように変化するわけじゃないのに、誰も理論式と数式の違いに気付かないまま、「２０世紀最大の発見」になってしまった。

「Ｅ=Ｍc^２は核反応で証明されている。質量の欠損がエネルギーに変換されたことは明らかだ」

物質がエネルギーに変換されるかどうかがテーマじゃないことはわかるよね。Ｅ=Ｍc^２で現実の物理現象を説明するのは式の検証が終わってからにしようよ。

この原因も含めてこの論文の問題点をザッとあげると・・・

• 理論式と数式を混同している
  
  理論式は任意の量で理論を展開できる代わりに、数量的な評価はしないもの。任意の量ではじめた仮想実験は係数を得た後、数式扱いする場合は初期設定の式に未知関数を記入する必要がある。
• ｃ^２が莫大な量だと勘違いしている
  
  ｃが光速度を表わすという前提から、ｃの二乗がもっと大きな数字になると思いたくなる。しかし、光速度ｃ以外の速度成分が存在しないＥ=Ｍc^２では、ｃは速度成分の存在を表す以上の数量的な意味を持たない。
• 単位系の採用を想定している
  
  式を評価する際に、単位系の選択が前提になってるが、質量とエネルギーを結びつける単位系が確立されているのなら、等価性は単位系の定義上で、すでに判明していることになる。
• Ｍは質量Ｍでなく運動量Ｍ1の省略形
  
  等式を維持するには左辺と右辺は同じ処理をしなければならない。運動量Ｍｖをｖで割る時、式の反対側Ｅ/ｃ^２を速度成分を含まない値ｖで割っている。運動量Ｍｖは速度成分を残したまま運動量Ｍとなるが、式の評価時は質量Ｍと解釈している。
• 片道だけに光速度不変を採用している
  
  静止系から運動系、運動系から静止系への設定変更のうち、光速度不変の原理が採用されているのは静止系から運動系へ輻射エネルギーを変換した１回のみ。
• 「質量＝エネルギー」が仮定されたまま終わっている
  
  座標変換の失敗でｃ^２が発生したことから、等価性も同時に証明されたと錯覚しているが、先に質量とエネルギーの等価性の証明を終了していなければ、係数の導出は不可能。
• エネルギー保存の法則の適用範囲が間違っている
  
  エネルギー保存の法則は系全体のエネルギーの総量について有効。輻射エネルギーのｚ方向のみでなく、全体のＥ/ｃに適用すると式は、当然、初期設定Ｍ＝Ｅ/ｃに戻ってしまう。
• なぜかｚ方向のエネルギーを取り出している
  
  物体Ｂに吸収され、質量に変換されたのは輻射エネルギーのｘ成分。輻射エネルギーのｚ成分は物体Ｂが静止してると解釈した時点で０になるため求める必要はない。
• 速度ｖで運動する座標系はいらない
  
  最終的に物体の運動速度ｖが入っていない式を評価するということは、運動速度に依存しない仮想実験が可能ということ。任意の速度ｖを一般化して速度１とした場合、ｖ/ｃ＝１/ｃとなる。１/ｃで掛けることは、輻射エネルギーのみを単純にｃで割ったことになる。
• 物質Ｂはいらない
  
  式の中では物質Ｂの質量増加分のみが残るように再定義されて、物質Ｂは消去されている。エネルギー同士が衝突して反応することを避けるために物体Ｂを想定したと思われるが、放射圧が物体を介在せずに直接対消滅することを前提とするなら、この時点で力の定義を拡大していることになる。
• 単位体積あたりの計算が二重になっている
  
  輻射エネルギーＥの単位体積あたりの輻射エネルギーがＥ/ｃなら、ｚ成分を算出する際、速度ｖを掛ければいいはず。ｖ/ｃで掛けるのは、単位体積あたりのエネルギーをさらに基本距離あたりのエネルギーに換算していることになる。
• 相対論と同じトリックを使ってる
  
  相対論の論文「運動する物体の電気力学について」と同じように、観測対象の移動方向と直角に移動する座標系を設定し、斜めに見える合成距離への変換に光速度不変の原理を応用。これを不完全に行うことで係数を発生させている。
• 成立条件はｖ＝ｃ、v≠c
  
  光速度不変の原理を採用すれば、輻射エネルギーの速度はｃとなる。物体Ｂは輻射エネルギーのｚ方向成分と並走しているためｖ＝ｃ。ｖ/ｃはｃ/ｃ＝１となる。またｖがｃに比べて小さいのという理論の条件下ではｖ≠ｃ。
• 光速度不変を採用すると崩れる
  
  輻射エネルギーの速度がｃであるなら、光速度不変の原理が適用されｘ、ｙ、ｚ方向の速度もｃとなる。作図では直角三角形の３辺がすべてｃになる。
• 相対論を否定している
  
  「２次の微小量（１に対してｖ^２/ｃ^２）を無視する」とは、相対論の変換式がガリレイ変換と等しいということ。この論文の成果が相対論と両立しないことを意味している。
• 相対性原理に反してる
  
  物体ＢとエネルギーＥの座標変換式が同一でない。
• 輻射のｚ成分と輻射複合体の運動成分を間違えてる
  
  物体Ｂに吸収される対象は速度ｃを持った輻射エネルギーそのもの。座標変換に使われているｖ/ｃは輻射エネルギーを発してる輻射複合体の動きのｚ成分。輻射エネルギーの計算に、エネルギー発生源の動きが採用されている。

上にあげた項目は、未検証のものや同時に成立しない項目もあるってことを頭のすみに置いといてね。科学者が主張をコロコロ変えないなら、この中の１つの指摘事項でＥ=Ｍc^２が架空の式だと証明できるよ。