1994擭偵摽娫彂揦偐傜弌斉偝傟偨亀乽憡懳榑乿偼傗偼傝娫堘偭偰偄偨亁偵宖嵹偝傟偨丄乽憡懳榑傪懪偪嵱偔僔儖僶乕僴儞儅乕乿傪岞奐偟傑偡丅
摉帪偼憡懳惈棟榑偑娫堘偭偰偄傞偲偄偆堄尒偼偛偔彮悢偱偟偨丅偟偐偟丄憡懳榑傪梚岇偟偰偄偨嫵庼偑榑攋偝傟丄彂愋偵師乆偵岆傝偑尒偮偐傞偲偟偩偄偵忬嫷偼媡揮偟偰偒傑偟偨丅堦斒偺恖乆偵傕暔棟妛傪榗傔偰偄傞憡懳榑偺巔偵婥晅偄偰傕傜偆偵偼丄杮峞偱弎傋偰偄傞傛偆側悢妛揑帠幚傪巜揈偡傞偙偲偑堦斣僔儞僾儖偱尰幚揑偩偲巚偄傑偡丅
偙傟偐傜婲偙傞暔棟妛偺曄妚偵偼壢妛幰偩偗偱側偔堦斒恖偺扤傕偑嶲壛壜擻偱偡丅偍偦傜偔暔棟妛偺婳摴傪惓忢偵栠偡嵟屻偺僠儍儞僗偱偟傚偆丅
憡懳榑傪懪偪嵱偔僔儖僶乕僴儞儅乕丂(1994)
杮峞偵娭偟偰偼,亀價僢僌僶儞棟榑偼娫堘偭偰偄偨亁乮僐儞僲働儞僀僠挊丂彫幮姧乯偺拞偱偡偱偵偦偺堦晹偑徯夘偝傟拲栚偝傟偰偄傞丅愱栧壠偐傜偼乽娭悢偺妵屖傗扨埵傪徣棯偟偰昞婰偡傞暔棟妛偺姷廗傪岆夝偟偨傕偺偱偼丠乿偲偺媈擮傕偁傞偑丆愱栧壠偱側偔堦斒恖偑憡懳榑傪妛傏偆偲偡傞嵺丆擔崅愢偺崪巕偼桳塿偱偁傞偲敾抐偟偰丆慡暥傪宖嵹偡傞偙偲偵偟傑偟偨乮曇廤晹拲乯丅
仸丂偙偺乽曇廤晹拲乿偼丄弌斉捈慜偵嶲壛梫媮偟偰偒偨抾撪孫巵偑娔廋偟偨愱栧壠偲曇廤晹椉曽傪墘偠偰憂嶌偟偨傕偺偱偡丅
丂徻嵶丂仜摉帠幰偩偐傜徹尵偱偒傞丅媈帡壢妛偺旐奞偵偁偭偨抾撪孫巵偺僨價儏乕懱尡択偼丄帺嶌帺墘両丂壢妛婾儔僀僞乕偑擔杮傪柵傏偡
僔儖僶乕僴儞儅乕偲偼壗偐
崱悽婭弶摢丄堦恖偺揤嵥偑敪昞偟偨憇戝側僷僘儖偼價僢僌僶儞傗僽儔僢僋儂乕儖丄偦偺懠懡偔偺妚柦揑梊尵偱塅拡暔棟妛偵傕戝偒側塭嬁傪梌偊傑偟偨丅偙偺夝摎偺側偄僷僘儖偼憡懳惈棟榑偲屇偽傟丄懡偔偺妛幰偵徧巀偝傟傞斀柺丄娤應偲棟榑偺憡堘偼俋侽擭戙偵擖偭偰偐傜傕傑偡傑偡怺崗偵側偭偰偄傑偡丅嫄妟偺旓梡傪偐偗偨憰抲偱偺専徹偑懕偗傜傟偰偄傞憡懳惈棟榑偼杮摉偵専徹偡傞壙抣偺偁傞棟榑側偺偱偟傚偆偐丅
偦偆偄偆巹偼憡懳惈棟榑傪媈偭偨偙偲偑堦搙傕偁傝傑偣傫丅傑偭偨偔棟夝偱偒側偐偭偨偺偱偡丅側偤娫堘偭偨幃傪巊偭偰偄傞偺偐丅側偤暔棟妛幰傑偱傕偑彫妛惗偱傕傢偐傞悢妛僩儕僢僋偵閤偝傟偰偟傑偆偺偱偟傚偆偐丅廗姷傗巚偄崬傒偱悢幃偺拞偺娭悢傪彑庤偵寛掕偟偰偄傞偺偑尨場偺侾偮偱偡偑丄偦偺帠幚傪擣傔偰傕傜偆偺偼梕堈側偙偲偱偼側偄傛偆偱偡丅
偦偺娭悢偺僩儕僢僋傪娙扨偵愢柧偟偰偍偒傑偡丅巹偨偪偼悢妛偺廗姷偲偟偰侾攞偵偡傞娭悢傪徣棯偟偰偄傑偡丅偙傟偐傜傑偭偨偔怴偟偄棟榑傪峫偊傛偆偲偡傞偲偒丄傕偟傕偦偺娭悢偵廋惓偑昁梫側傜偽徣棯偣偢偵幃偵婰擖偟偰偍偒傑偡丅偟偐偟偦偺懚嵼偦偺傕偺偵婥偯偄偰偄側偗傟偽娭悢偼亊侾偺傑傑幃偺拞偵暣傟崬傫偱丄幃慡懱傪榗傔偰偟傑偄傑偡丅偦偟偰丄偲偰傕忢幆偱偼棟夝偱偒側偄偍偐偟側棟榑偑偱偒忋偑偭偰偟傑偄傑偡丅憡懳惈棟榑偙偦偼偙偺傛偆側僩儕僢僋傪偄偔偮傕巊偭偰偱偒偨埆偄尒杮偩偲偄偊傑偡丅
傕偟棟榑偑峔抸偝傟偨偁偲偱尒棊偲偝傟偰偄偨娭悢偑敪尒偝傟傞偲丄堦弖偵偟偰棟榑偼曵夡偟偰偟傑偄傑偡丄偙偺傛偆偵棟榑偵偲偭偰嫼埿偲側傞娭悢傪偙偙偱偼乽僔儖僶乕僴儞儅乕乿偲屇傃傑偡丅巹偨偪偼崅摍幃偵婥傪庢傜傟丄俋侽擭偵傕偍傛傇憡懳惈棟榑偺楌巎偺杦偳傪栚偵尒偊傞幃偺専徹傗奼挘偵旓傗偟偰偒傑偟偨丅偟偐偟丄偦偆偟偰偄傞偡偒偵乽僔儖僶乕僴儞儅乕乿偼憡懳惈棟榑傪曔偊傞僠儍儞僗傪偆偐偑偭偰偄傑偟偨丅偦偟偰悑偵偦偺堦寕偑崀傝壓傠偡偝傟傛偆偲偟偰偄傑偡丅
俀侽悽婭嵟崅偺媈帡壢妛丄憡懳惈棟榑偑偁偭偗側偄傎偳娙扨偵懪偪嵱偐傟傞巔傪栚偺慜偵偟偰丄偦傟偱傕偁側偨偼帺慠偺朄懃傪憡懳惈棟榑偵媮傔傞偱偟傚偆偐丅偦傟偲傕棟榑傪婞偰嫀傞偱偟傚偆偐丅
偙偺彫榑偱偼偝傑偞傑側宍偺乽僔儖僶乕僴儞儅乕乿傪徯夘偟傑偡丅傑偢丄
- 侾丂楌巎揑側俤亖俵們俀偑堦斒偵抦傜傟偰偄傞傛偆側廳梫側堄枴傪慡偔帩偭偰偄側偄偙偲傪愢柧偟傑偡丅
- 俀丂摿庩憡懳惈棟榑偑娭悢偺徣棯傪棙梡偟偨悢妛僩儕僢僋偱偁傞偙偲傪帵偟傑偡丅
- 俁丂嵟屻偵棟榑傪幚徹偟偨儅僀働儖僜儞乕儌乕儗乕偺幚尡寢壥偑幚偼屆揟椡妛傪巟帩偟偰偄傞偙偲傪娙扨偵愢柧偟傑偡丅
俀侽悽婭嵟戝偺敪尒
偙傟傎偳桳柤偱悽娫偵徴寕傪梌偊偨幃偼偼偐偵側偄偱偟傚偆丅乽傢偢偐側幙検偑敎戝側僄僱儖僊乕偵摍偟偄乿偲偄偆妚柦揑敪尒偵傛偭偰廬棃偺僄僱儖僊乕栤戣偼堦婥偵夝寛偝傟傞偲偝偊尵傢傟偰偄傑偡丅暔棟妛夛偱擣傔傜傟偨幃偼懡偔偺尋媶幰偲朿戝側帒嬥偵傛偭偰幚梡壔傊偺摴偑扵傜傟偰偄傑偡偑丄俤亖俵們俀偵廬偭偨暔棟尰徾側偳偼偙偺悽偵懚嵼偟側偄偲巹偼巚偄傑偡丅
侾俋侽俆擭侾俋係俇擭偵敪昞偝傟偨傢偢偐悢儁乕僕偺榑暥乽幙検偲僄僱儖僊乕偺摍壙惈偺弶摍揑徹柧乿偼僄僱儖僊乕偲幙検偵娭偡傞幚尡僨乕僞傪堦愗梡偄偢偵丄壖憐幚尡偩偗偱俤亖俵們俀傪摫偒弌偟偰偄傑偡乮姫枛帒椏俀嶲徠乯丅忢幆揑偵峫偊偰僨乕僞傪尒側偄偱娭學幃偑摫偒弌偣傞偼偢偑偁傝傑偣傫丅偄偐偵揤嵥偲偄偊偳傕壖憐偐傜恀幚傪徹柧偡傞偺偼晄壜擻偱偡丅側偵偐僩儕僢僋偺傛偆側傕偺傪巊偭偨偲峫偊傞曽偑帺慠偱偼側偄偱偟傚偆偐丅俤亖俵們俀偑擇乑悽婭嵟崅偺暔棟幃偐偦傟偲傕僩儕僢僋偐偼丄偙偺榑暥傪拲堄怺偔撉傔偽扤偱傕暘偐傝傑偡丅傑偢偼偙偺専徹偐傜巒傔傞偙偲偵偟傑偟傚偆丅
壖掕偺崻嫆

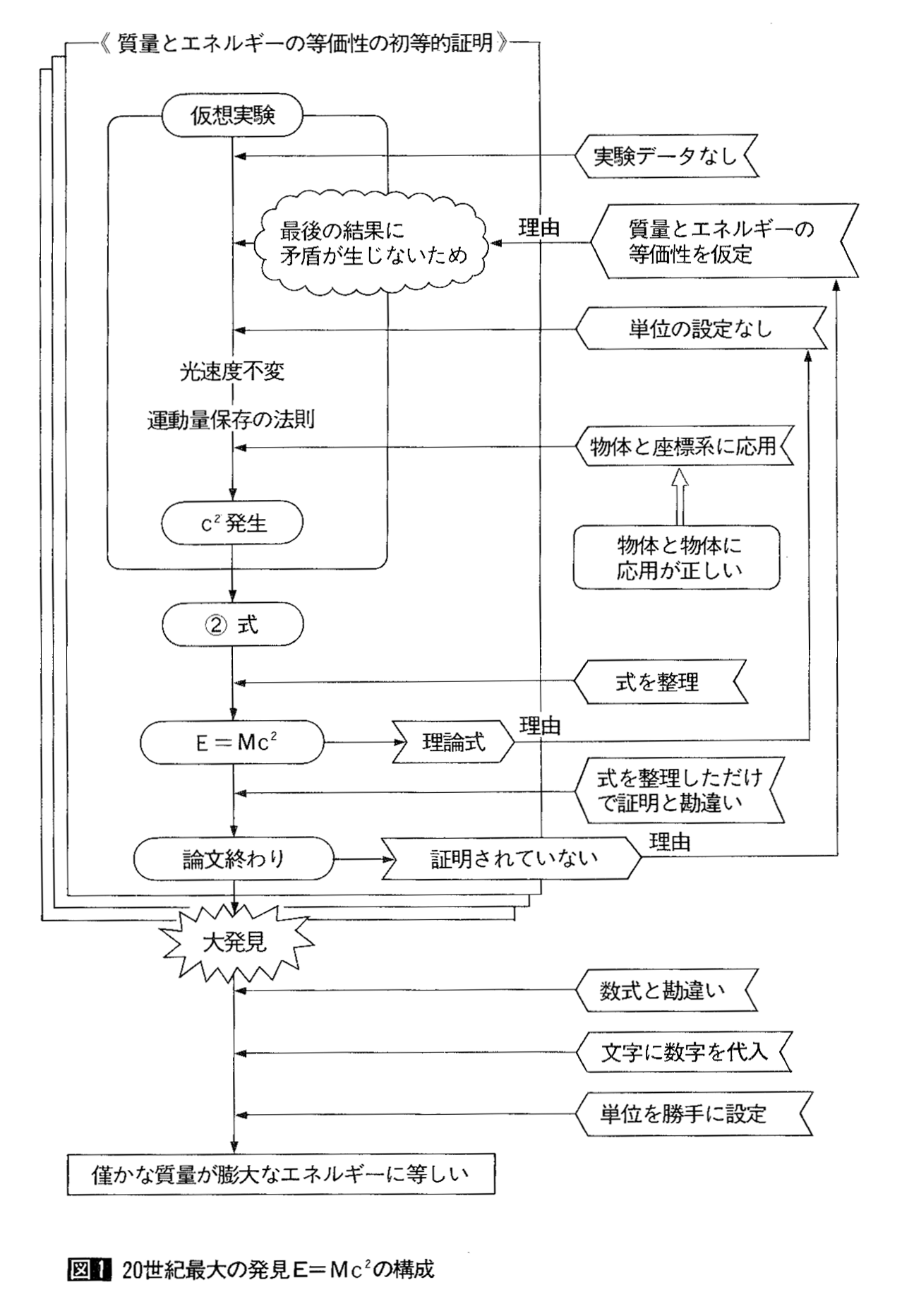
偙偺榑暥偵偼敳偒彂偒偝傟偨師儁乕僕偺幃偑係偮偁傞偩偗偱偡丅恖椶偺楌巎偑偙偺偨偭偨巐偮偺幃偵嵍塃偝傟偨偲巚偆偲晄巚媍側婥偑偟傑偡丅偱偼偦偺拞偺嘇幃偵拲栚偟偰偔偩偝偄丅偙偺幃傪彂偒姺偊傞偲俤亖俵們俀偵側傞偺傪妋擣偟偰偍偒傑偡丅
- 椉曈傪円偱妱傞偲丄
俵亄乮俤乛們俀乯亖俵丩丄 - 俵傪堏崁偟偰丄
俤乛們俀亖俵1亖俵丩亅俵 - 俵丩亅俵傪俵1偲偡傟偽丄
俤乛們俀亖俵1 - 俤偵偮偄偰偺幃偵偡傟偽丄俤亖俵1們俀傑偨偼偙傟傪堦斒壔偟偰丄
俤亖俵們俀
乽暔懱偺塣摦検俵円偲鐃幩暋崌懱俽丄俽丩偺塣摦検乮俤亖俵們俀乯円偵側傞乿
偙偺壖憐幚尡偺寢壥偼偄偭偨偄壗張偐傜摼傜傟偨偺偱偟傚偆偐丅恖椶偺楌巎偵巆傞執戝側敪尒偺堿偵偼抧摴側娤應傗幚尡偑偁偭偰偟偐傞傋偒偱偡丅偲偙傠偑榑暥偵偼偦偺傛偆側僨乕僞偼堦愗偁傝傑偣傫丅幚偼偙偺寢壥偼幚尡僨乕僞偑側偄偐傜壖掕偟偨傕偺側偺偱偡丅偦偺壖掕偲偼丄乽幙検俵偵僄僱儖僊乕俤偑媧廂偝傟偨偺偪丄幙検俵丩偵憹壛偟偨偲壖掕偡傞乿偲偄偆傕偺偱偡丅偮傑傝丄嘇幃偼幙検偲僄僱儖僊乕偺摍壙惈傪嵟弶偵婰弎偟偨幃偩偭偨偺偱偡丅偦偟偰榑暥偼俤亖俵們俀偑摫弌偝傟偨偲偙傠偱廔傢偭偰偄傑偡丅
壖掕偟偨幃傪曄宍偟偨偩偗偱徹柧傪廔椆偟偰偄傞偺偱偡丅幙検偲僄僱儖僊乕偺摍壙惈傪壖掕偟偰丄俤亖俵們俀傪摫偄偰傕幙検偲僄僱儖僊乕偺摍壙惈傪徹柧偟偨偙偲偵偼側傝傑偣傫丅捁偺僸僫傪彫將偲壖掕偡傟偽傗偑偰將偑嬻傪旘傋傞偙偲偑徹柧偝傟傞偱偟傚偆偑丄捁偺僸僫偑彫將偩偲偄偆徹柧偑偝傟側偗傟偽摼傜傟偨寢壥偼扨側傞壖掕偱偡丅偮傑傝俤亖俵們俀偼妋棫偝傟偨棟榑偐傜摼傜傟偨寢榑偱偼側偔壖掕偝傟偨忦審傪梫栺偟偨棟榑幃偵偡偓側偄偲偄偆偙偲偱偡丅偦偺徹嫆偵榑暥偵偼壖掕偺崻嫆偑乽峫嶡偺嵟屻偺寢壥偵柕弬偑惗偠側偄偨傔偵昁梫偱偁傞乿偲柧婰偝傟偰偄傑偡丅
寢嬊丄乽僄僱儖僊乕偲幙検偺摍壙惈乿偼俤亖俵們俀傪惉棫偝偣傞偨傔偵壖掕偝傟偨偩偗偱丄寛偟偰徹柧偝傟偨傕偺偱偼側偄偺偱偡丅壖掕傪曄宍偝偣偰徹柧偵棙梡偡傞偙偺傛偆側曽朄偼摿庩憡懳惈棟榑偺榑暥偱傕巊傢傟偰偄傞庤朄偱丄拲堄偟偰撉傑側偄偲偮偄擺摼偝偣傜傟偰偟傑偄偦偆偵側傝傑偡丅偙偺徹柧朄傪巊偊偽將僝儕偵忔偭偰寧偵峴偔偙偲傕壜擻偵側傞偱偟傚偆丅
棟榑幃偺棊偟寠
懡偔偺壢妛幰偑偙偺幃偵嬃扱偟偨偺偼幙検俵偵們俀偑偮偄偰偄偨偐傜偱偡丅們俀偵朿戝側悢抣傪戙擖乽嬐偐側暔懱偐傜朿戝側僄僱儖僊乕乿偑庢傝弌偣傞偲敾抐偟丄偨偭偨侾偮偺僕儍僈僀儌偱抧媴偺僄僱儖僊乕婋婡傪媬偆偙偲傪柌尒偰偄偨偺偱偡丅奺崙偺孯帠椡僶儔儞僗偑僇儃僠儍傗僯儞僕儞偱寛傑傝丄媿偺僼儞傑偱傕偑揋崙偺嫼埿偲側傝偊傞偺偱偡丅
俤亖俵們俀偼壖掕偟偨暔棟揑堄枴傪婰弎偟偨偩偗偺棟榑幃偵偡偓傑偣傫丅検揑梫慺傪傑偭偨偔娷傫偱偄側偄偺偱扨埵傗悢抣傪擖傟偰巊偆偙偲偼偱偒側偄偺偱偡丅幃偺墳梡斖埻傪墇偊偰偟傑偆偐傜偱偡丅僆乕儉偺朄懃乮俬亖倁乛俼乯偵岲偒彑庤側扨埵偲悢帤傪擖傟偰巊偭偰偄傞恖偼偄側偄偱偟傚偆丅俤亖俵們俀傕摨偠偱丄悢幃偺傛偆側巊偄曽傪偟偰偼偄偗側偄偺偱偡丅榑暥偺偳偙偵傕扨埵傗検傪愝掕偟偰偄傞売強偼偁傝傑偣傫丅幙検偲摍壙偺僄僱儖僊乕偑扨埵偺慖傃曽偱曄壔偡傞偺偼偙傟偑検揑梫慺傪慡偔娷傫偱偄側偄棟榑幃偩偐傜偱偡丅
壖偵丄悢幃偲偟偰傕堦斒揑側偲傜偊曽偵偼戝偒側姩堘偄偑偁傝傑偡丅師偺悢幃傪尒偰偔偩偝偄丅
亹1亖亸侾侽侽
侾僪儖亖侾侽侽墌傪昞偟偰偄傑偡丅偙偙偱亹丄亸偼扨埵乮娭悢乯偱偡丅侾侽侽攞偟偰偄傞墌偺偼偆偑摉慠彫偝側扨埵偲偄偆偙偲偼恎嬤側宱尡偐傜傕傢偐傝傑偡丅俤亖俵們俀偑悢幃偩偲偡傞偲俤偼俵傛傝們俀攞戝偒側扨埵偩偲偄偊傑偡丅偙偺揰偵婥傪偮偗偰俤亖俵們俀偺堄枴傪愢柧偡傟偽丄
乽幙検偺扨埵俵偲們俀攞戝偒偄僄僱儖僊乕偺扨埵俤偱僄僱儖僊乕偲幙検偺摍壙惈傪壖掕偡傟偽俤亖俵們俀偲側傞乿
側傫偲偁偨傝傑偊側傫偱偟傚偆偐丅墌偐僪儖偵姺嬥偱偒傞偲壖掕偟偨偩偗偱偼姺嶼儗乕僩偑傢偐傜側偄傛偆偵丄僄僱儖僊乕偲幙検偺摍壙惈傪壖掕偟偨偩偗偱偦偺斾棪傑偱偑傢偐傞偼偢偑側偄偺偱偡丅俵偑壗攞偝傟傛偆偲傕椉曈偑摍偟偄偺偩偐傜丄扨埵偑曄壔偡傞偩偗偱偡丅幃偺曄壔暘偑偡傋偰乽扨埵乿偺曄壔偵媧廂偝傟偰偟傑偆偺偱偡丅偙偺尨場傕榑暥偺側偐偱扨埵傪愝掕偟側偐偭偨偐傜偱丄扨埵偑敾柧偡傞傑偱娭悢昞帵偵偟偰偍偗偽偙偺傛偆側偙偲偼婲偙傝摼側偐偭偨偱偟傚偆丅扨埵偼曄傢傜側偄傕偺偲偄偆愭擖娤偑俤亖俵們俀傪傛傝堦憌楌巎揑側戝敪尒偵偟偰偄傞帠幚傕尒摝偣傑偣傫丅
偦傟偱傕憡懳惈棟榑丠
侾俋侽俆擭偵乽塣摦偟偰偄傞暔懱偺揹婥椡妛偵偮偄偰乿偲偄偆榑暥偑敪昞偝傟傑偟偨丅尰嵼偺暔棟妛傗塅拡榑偺婎慴偲側傞憡懳惈棟榑傪悽偵憲傝弌偟偨桳柤側榑暥偱偡乮姫枛帒椏俁嶲徠乯丅俀侽悽婭偺暔棟妛傪崿柪偝偣丄崱側偍懡偔偺暔棟妛幰偵傛偭偰巟帩偝傟偰偄傞憡懳惈棟榑丅偡傋偰偼偙偺榑暥偱巒傑傝傑偟偨丄俋侽擭傕偺娫丄懡偔偺桪廏側摢擼偵傛偭偰専徹偟恠偔偝傟偨偼偢偺棟榑偵岆傝偑偁傞偺偱偟傚偆偐丅偙偺棟榑傪敪昞偟偨恖暔偑堄奜偵傕彫妛峑帪戙偵棊偪偙傏傟偱嶼悢偑嬯庤偩偭偨偙偲偑桳椡側僸儞僩偱偡丅岆傝偑偁傞偲偡傟偽崅摍幃傛傝傓偟傠弶摍幃偵偁傞偲峫偊丄榑暥偺弶婜愝掕偵拝栚偡傞偺偑夝摎傊偺戞堦曕偲側傝傑偡丅

榑暥偵偼俀侽侽傕偺暥帤幃偑搊梘偟傑偡偑丄偙偙偱専徹偡傞偺偼朻摢偐傜俋偮栚偺幃傑偱偱偡丅偦傟傜偺弶摍幃偼嶼悢偺抦幆偩偗偱棟夝偱偒傞傎偳娙扨偱偁傝側偑傜丄憡懳惈棟榑偺惈幙傪寛掕偯偗偰偄傞岆傝偑婔偮傕媗傔崬傑傟偰偄傑偡丅偦傟埲崀偺幃偼擄夝偱棟榑偺惓斲傪敾抐偡傞偵偼偁傑傝嶲峫偵側傜側偄偱偟傚偆丅憡懳惈棟榑偺専徹偵昁梫側偺偼敎戝側帒嬥傪偐偗偰寶愝偝傟偨専徹憰抲側偳偱偼側偔丄偨偭偨侾枃偺巻偲墧昅偱廫暘側偺偱偡丅
娭悢幃偺僩儕僢僋
傑偢娭悢傪巊偭偨娙扨側僩儕僢僋傪愢柧偟傑偡丅捠忢丄娭悢偼倖亖倎乮倶乯偺傛偆偵婰弎偝傟傑偡丅偙偺応崌丄娭悢倖偼僨乕僞倶傪倎攞偵偡傞娭悢偱偡丅偙偺婰弎曽朄偱偼僨乕僞倶傪妵屖偺拞偵擖傟偰偍偒丄娭悢倖偱曄姺偟側偗傟偽懠偺悢抣偲寁嶼偱偒側偄傛偆偵偟傑偡丅偙傟偼悢妛偺婎杮揑寛傑傝偱偁傝丄廗姷偱傕偁傝傑偡丅扨弮偵峫偊偰娭悢倖偼梌偊傜傟偨僨乕僞傪倎攞偡傞堦師娭悢偲尷掕偟偰丄攞悢偲摨偠偔埖偭偰傕傛偝偦偆偱偡丅偦偟偰攞悢側傜偽摨偠娭悢暥帤偑偮偄偨僨乕僞偳偆偟偼寁嶼偟偰傕嵎偟巟偊側偄偱偟傚偆丅
偙偙偱(8)幃傪尒偰偔偩偝偄丅冄偼倶丩丄倷丄倸丄倲偺娭悢偲掕媊偝傟偰偄傞偺偱丄暣傟傕側偔冄偼娭悢偱偡乮偙偺枹抦偺娭悢冄傪媮傔傞偺偑榑暥偺栚揑偱偡乯丅(8)幃偵偼娭悢冄偲偦傟偧傟偺妵屖偵擖偭偨僨乕僞偑嶰慻偁傝傑偡丅(8)幃偺倶丩傪柍尷彫偵偲偭偰愭傎偳偺峫偊偱宍傪曄偊偨偺偑(9)幃偱偡丅偙偺幃偺塃曈偵偼娭悢冄偺妵屖乮丂乯偑偁傝傑偣傫丅嵍曈偵偼妵屖偑偁傝傑偡偑丄娭悢偺僨乕僞傪擖傟傞妵屖偱偼側偔丄寁嶼偺弴彉傪昞偡偲偒偺妵屖偱偡丅偮傑傝(9)幃偵偼僨乕僞傪擖傟傞妵屖偼侾偮傕側偄偙偲偵側傝傑偡丅(8)幃偺僨乕僞傪寁嶼偟偨偺偱妵屖偼偄傜側偔側偭偨偺偱偡丅
偍偐偟偄偲巚偄傑偣傫偐丠丂榑暥偼枹抦偺娭悢冄傪媮傔傞偨傔偵恑傔傜傟偰偄傞偺偱偡丅偦偺峔惉偑敾柧偟偰偄傞偺偼(8)幃傛傝偝傜偵屻偺俆侾斣栚偺幃偱丄偙傟偐傜娭悢冄傪媮傔傛偆偲偟偰偄傞(9)幃偺妵屖傪奜偣傞偼偢偑側偄偺偱偡丅娭悢冄偑攞悢偺傛偆側堦師娭悢側傜壜擻偱偡偑丄傕偟堦師娭悢側傜憡懳惈棟榑偼屆揟椡妛偵婣寢偟偰偟傑偄傑偡丅
偙偙偱壗偑峴傢傟偨偐偲偄偆偲丄乽娭悢偺妵屖偲攞悢偵晅偗傞妵屖偲傪娫堘偭偰拞恎傪寁嶼偟偰偟傑偭偨乿傑偨偼乽枹抦娭悢冄傪堦師娭悢偺媮傔曽偱偩偟偰偟傑偭偨乿偺偱偡丅曮扵偟偵峴偔偲尵偭偰嬧峴偺抧恾傪尒傟偽曮偼昁偢尒偮偐傞偱偟傚偆丅枹抦娭悢傪媮傔傞岞幃偑懚嵼偟側偔偰傕娭悢冄偑媮傔傜傟偨偺偼娫堘偭偨曽朄傪巊偭偨偐傜偱偡丅偙傟偱(9)幃埲崀偺崅摍幃傪専徹偟側偔偰傕傛偄棟桼偑偍傢偐傝偵側偭偨偺偱偼側偄偐偲巚偄傑偡丅
摨帪偺弌棃帠
丂乽塣摦宯內偺尨揰偐傜岝慄偑帪娫恲偵倃幉偵増偭偰倶丩傑偱曻幩偝傟丄帪娫冄1偵斀幩偝傟偰帪娫冄2偺尨揰偵栠偭偨乿丅偙傟傪岝懍搙晄曄偺傕偲偱幃偵偟偨偺偑(7)幃偱偡丅嵍曈偼墲暅偵偐偐偭偨帪栤丄塃曈偼墲楬偵偐偐偭偨帪娫偱丄塣摦宯偱偼墲楬偲暅楬偵摨偠帪娫偑偐偐偭偨偙偲偑愭摢偺1乛俀偵尰傟偰偄傑偡丅摨偠帠審傪掕忢宯偐傜婰弎偡傞偲(8)幃偵側傝傑偡丅傗偼傝嵍曈偼墲暅偵偐偐偭偨帪娫丄塃曈偼墲楬偵偐偐偭偨帪娫偱偡丅偦偟偰偙偙偱傕愭摢偵偼侾乛俀偑晅婰偝傟偰偄傑偡丅偮傑傝(8)幃偱傕墲楬偲暅楬偵摨偠帪娫偑偐偐偭偨偙偲偵側偭偰偄傑偡丅俀偮偺幃偑摨偠宍傪偟偰偄傞偺偼帠審偑摨帪偵婲偙偭偨偙偲傪昞偟偰偄傑偡丅摨偠帠審傪堎側偭偨嵗昗宯偱尒偨偩偗側偺偱丄巹偨偪偺忢幆偳偍傝偵掕忢宯偲塣摦宯偺弌棃帠偼摨帪偵婲偙偭偨偲夝庍偟偰傕偄偄偺偱偟傚偆偐丠
榑暥傪屛傞偲憡懳惈棟榑偺昁梫惈傪愢偔偨傔偵摨帪惈偺奣擮偑岝懍搙晄曄偺忦審壓偱捠梡偟側偄偙偲偑愢柧偝傟偰偄傑偡丅摨偠弌棃帠偑嵗昗宯偺堘偄偱摨帪偱偼側偔側傞偲偄偆婏柇側庡挘偱偡丅偙偺庡挘傪庢傝擖傟傟偽(7)幃偲(8)幃偼摨帪偵婲偙偭偨帠審偱偼偁傝偊側偄偺偱偡丅摝偘傞揇朹偲偡傟堘偆傛傝捛偄偐偗傞曽偑帪娫偑偐偐傞傛偆偵丄塣摦偟偰偄傞慄暘忋傪岝偑墲暅偡傟偽暅楬傛傝傕墲楬偵帪娫偑偐偐傝丄塣摦宯偺婰弎偲偼堦抳偟側偔側傝傑偡丅偮傑傝掕忢宯偱偼丄侾乛俀偵偼側傜偢枹抦偺娭悢偵側傝傑偡丅(8)幃偺侾乛俀偼嵗昗曄姺偵偆偭偐傝偟偰摨帪惈偺奣擮傪巊偭偰偟傑偭偨側偛傝偱偡丅偙偺奣擮傪巊傢側偄偲嵗昗曄姺偺曽朄偑傑偩尒偮偐偭偰偄側偄偺偱偙傟埲忋愭偺幃偵偼恑傔側偐偭偨偼偢偱偡丅
曄壔偡傞暔嵎偟
乽塣摦偡傞朹俙俛偱岝偑俙揰偐傜帪崗倲俙偵弌敪偟丄倲'俙偵俛揰偱斀幩偟偰丄帪崗傜偵嵞傃俙偵栠偭偨乿偲
偄偆愝掕偱丄岝懍搙晄曄偺尨棟偱偼丄朹偲摨偠塣摦宯偺娤應幰偼墲楬偲暅楬偼摨偠帪奐偐偐偐偭偨偲庡挘偟丄掕忢宯偵偄傞娤應幰偼丄墲楬偑(4)幃丄暅愓偑(5)幃偵側傞偲庡挘偟傑偡丅偮傑傝墲暅偺帪栤偵怘偄堘偄偑弌傞偲偄偆偺偱偡丅偙偺俀偮偺幃偼屆揟椡妛偺摨帪惈偺奣擮傪斲掕偡傞偨傔偵巊傢傟偰偄傑偡偑丄杮棃岝懍搙晄曄偲僈儕儗僀曄姺偼娭學偺側偄傕偺偱偡丅岝偺懍搙傪乮們亅円乯傗乮們亄円乯傪巊偭偰僈儕儗僀曄姺偟偰偄傞偐傜摨帪惈偑曵傟偰偟傑偭偨偺偱丄晄巚媍側偙偲偱偼偁傝傑偣傫丅
岝懍搙偑偄偐側傞嵗昗宯偱傕堦掕側傜偽岝懍搙偼掕悢偱偡偑丄乮們亅円乯傗乮們亄円乯偱憡懳懍搙傪媮傔偰偄傞岝懍搙偼曄悢偲偄偊傑偡乮憡懳惈棟榑偺岝懍搙偼偄偭偨偄偳偪傜偱偟傚偆偐乯丅榑暥偱偼岝傪摿暿側傕偺偲壖掕偟偨偵傕偐偐傢傜偢幃偺揥娫偱懠偺傕偺偲崿偤偰偄傑偡丅偙傟偑掕悢偲曄悢傪僀僐乕儖偱寢傇栶妱傪壥偨偟偰僷儔僪僢僋僗傪嶌偭偰偄傞偺偱偡丅偙偺揰偵偮偄偰乽憡懳惈棟榑偼屆揟椡妛偺廋惓棟榑偩偐傜偄偄偺偩乿偲傛偔斀榑偝傟傑偡偑丄娭悢冄偼塣摦宯偐傜掕忢宯傊偺曄姺娭悢偱偡丅寛偟偰屆揟椡妛偐傜憡懳惈棟榑傊偺曄姺娭悢偱偼側偄偺偱偡丅傑偨乽屆揟椡妛偼嬤帡偩乿偲偄偆憡懳惈棟榑偺庡挘偼嬤帡傪巊偭偰惓夝傪媮傔偨偙偺棟榑偺悢妛揑寚娮傪棤偯偗偰偄傑偡丅
偝偰丄(4)幃丄(5)幃傪暿偺愝掕偵偟偰塣摦偡傞朹偺挿偝傪岝偱應偭偨揰傪専徹偟偰傒傑偟傚偆丅扤偐傜尒偰傕堦掕偺傕偺偑應掕偺庤偑偐傝偵側傞偺偱偟傚偆偐丅偄傑憱偭偰偄傞僿價傪偲傕偵堏摦偟偰偄傞娤應幰俙偑侾侽儊乕僩儖偺暔嵎偟偱應傞偲偟傑偡丅嵟弶偵僿價偺摢傪丄偦偟偰侾昩屻偵僔僢億偺枛抂偺栚惙傝傪撉傒庢傞偲僿價偺挿偝偑寁嶼偱偒傑偡丅
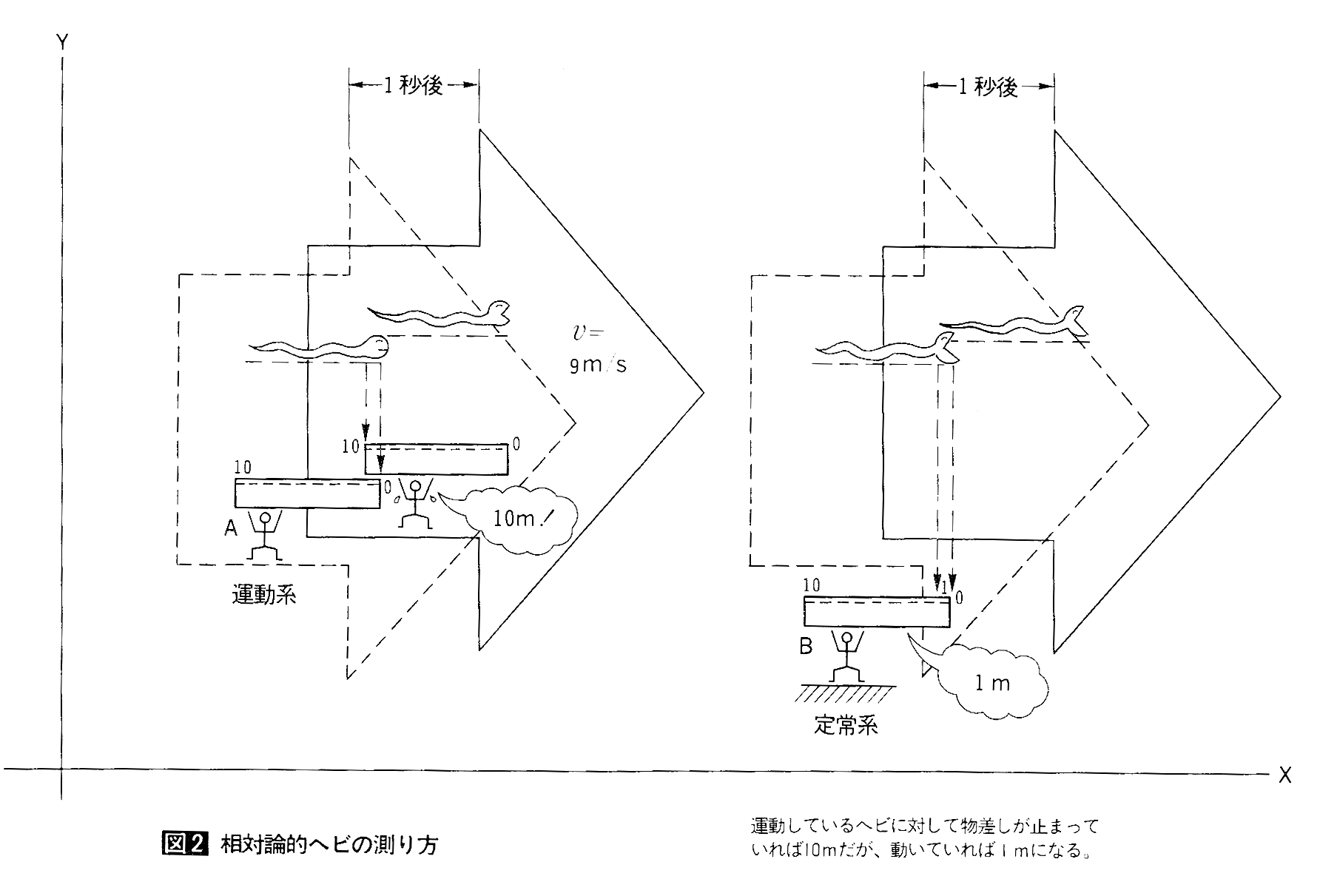
俙偐傜尒傞偲僿價偲暔嵎偟偺憡懳懍搙偼侽偱偡丅塣摦宯偺娤應幰俙偼應掕偑廔傢傞偲僿價偼偪傚偆偳侾侽儊乕僩儖偺戝幹偩偲尵偄巆偟偰堦栚嶶偵摝偘弌偟傑偟偨丅偦傟傪暦偄偨掕忢宯偺娤應幰俛偑棊偪偰偄偨暔嵎偟傪庤偵庢傝憱偭偰偄傞僿價傪應傝傑偟偨丅俛偐傜尒傞偲僿價偲暔嵎偟偺憡懳懍搙偼昩懍俋儊乕僩儖偱偡丅僿價偺摢偺栚惙傝傪撉傒庢偭偰偐傜侾昩偺娫偵僿價偺僔僢億偼暔嵎偟偺愭抂曽岦傊俋儊乕僩儖堏摦偟偨偺偱丄俛偼僿價偺挿偝傪侾儊乕僩儖偩偲庡挘偟傑偟偨丅椉幰偐傜傒偰堦掕偺暔嵎偟偱摨偠僿價傪應偭偨偵傕偐偐傢傜偢應掕抣偵嵎偑偱偰偟傑偄傑偟偨丅偙偺傛偆偵岝偱側偔偲傕憡懳惈棟榑偲摨偠傛偆側尰徾偑婲偙傞偺偼乽婎弨偲應掕懳徾偑摦偄偨乿偐傜偱丄應掕曽朄偵栤戣偑偁傞偺偱偡丅暔嵎偟偼俙丄俛偳偪傜偵偲偭偰傕堦掕偵尒偊偰傕僿價偵偲偭偰堦掕偱側偗傟偽堄枴偑側偄偺偱偡丅摉慠丄應掕偵帪娫傪偐偗傞傎偳岆嵎偼戝偒偔側傝傑偡丅
應掕偵帪娫傪偐偗傞戙傢傝偵岝偺懍搙傪婎弨偵偟偨偺偑憡懳惈棟榑偱偡丄尵偆傑偱傕側偔應掕懳徾偲岝偼摦偄偰偄傞偺偱愭偺忦審傪摨帪偵枮偨偣傑偡丅偙偺棟榑偑昁偢扤偐傜尒偰傕堦掕偺岝偱傕偺傪應傞偺偼偙偺僩儕僢僋傪巊偆偨傔偱偡丅偙偺愢柧傪暦偄偰傕僿價偵堸傒崬傑傟偨娤應幰俛偼偙偆尵偭偰戝婌傃偡傞偱偟傚偆丅乽恎挿俀儊乕僩儖偺偙偺壌偑侾儊乕僩儖偺僿價偺暊偵廂傑傞偺偼偒偭偲憡懳榑揑岠壥偵堘偄側偄乿偲丅
懍搙偺岞幃
巹偨偪偼嬻娫傪悢妛揑偵庢傝埖偆偨傔偵捈岎偡傞倶幉丄倷幉丄倸洬傪愝掕偟偰偄傑偡丅偟偨偑偭偰丄嬻娫偺偁傞堦揰傪婰弎偡傞偵偼俁偮偺僨乕僞偑昁梫偱偡丅傕偟侾偮偱傕寚偗偰偄傟偽丄嬻娫撪偺偁傞堦揰偼偄偮傑偱傕尷掕偱偒偢丄悢抣寁嶼偼偱偒傑偣傫丅傑偨丄侾偺僨乕僞傪扨撈偱埖偆偙偲傕偱偒傑偣傫丄偙傟偼偦傟偧傟偺僨乕僞偑僺僞僑儔僗偺掕棟偵婎偯偄偨曄姺偱摑崌偝傟偰偼偠傔偰侾偮偺悢抣偲傒側偝傟傞偙偲偵傛傝傑偡丅
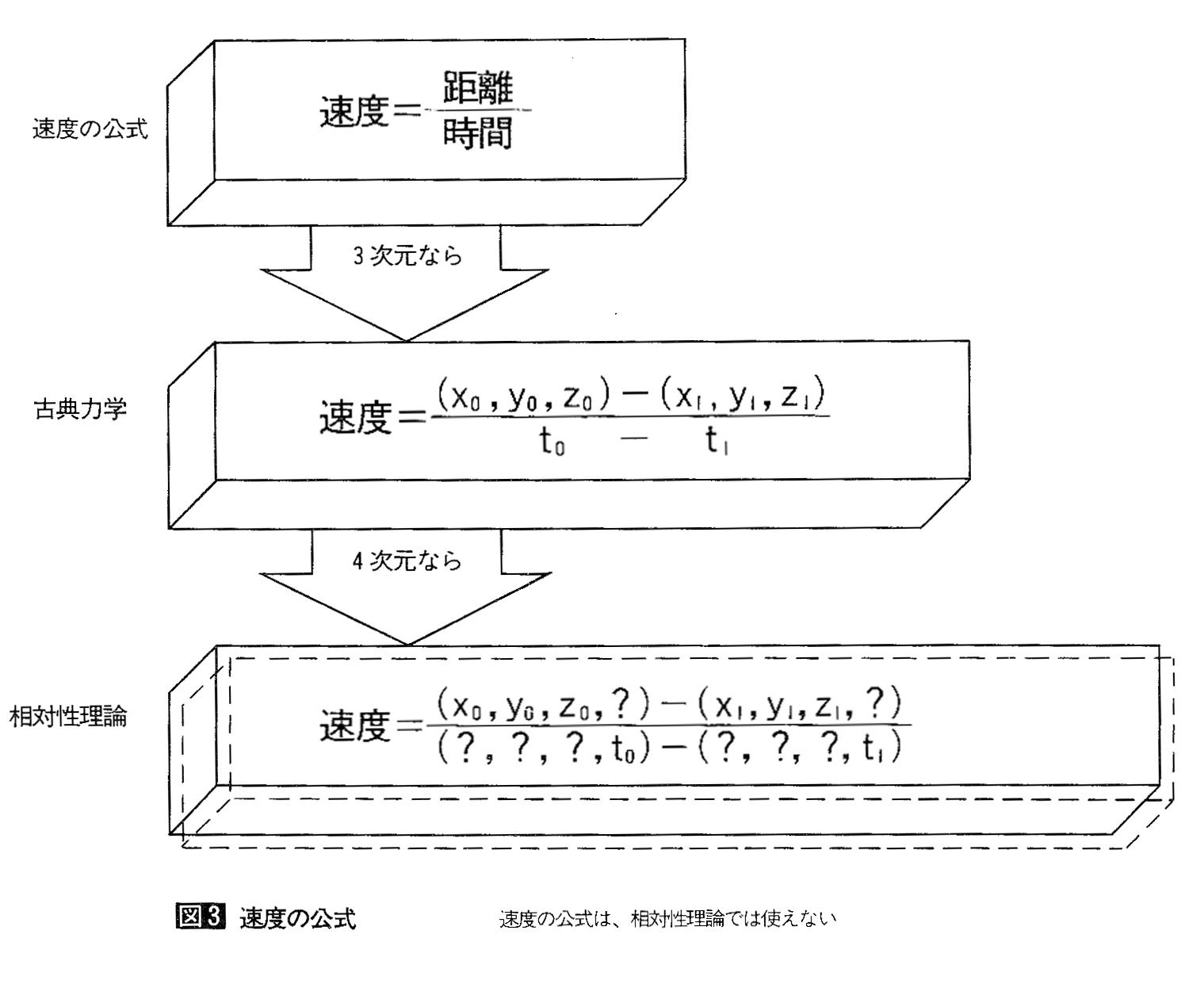
憡懳惈棟榑偱偼偳偆偱偟傚偆偐丅嶰師尦偵帪娫惉暘倲傪壛偊偰係偮偺僨乕僞傪傂偲慻偵偟偰侾揰傪昞偟偰偄傑偡丅(8)幃偺娭悢冄偵擖偭偰偄傞僨乕僞乮倶丄倷丄倸丄倲惉暘乯偑係偮偁傞偺偼偦偺偨傔偱偡丅偙偺棟榑偱帪栤偲嫍棧傪愗傝棧偟偨寁嶼傪偡傟偽摉慠丄曄姺傪偝傟偰偄側偄丄偁傞偄偼僨乕僞偺懙偭偰偄側偄嵗昗抣傪偦偺傑傑嫍棧偵抲偒姺偊偨偙偲偵側傝丄幃偵榗傒偑惗偠傑偡丅偟偐偟丄棟榑偱偼帪娫丄懍搙丄嫍棧傪撈棫偟偨僷儔儊乕僞偲偟偰埖偭偰偄傑偡丅嫍棧傪寛掕偡傞偵偼倶丄倷丄倸偺嶰梫慺丄帪娫傪寛掕偡傞偺偼倲偩偗偱偡丅
(3)幃傪尒偰偔偩偝偄丅偙偺幃偵塣摦懍搙円偑娷傑傟偰偄側偄偺偼丄掕忢宯偱岝偵懳偟偰偩偗巊偊傞娭學幃偱偁傞偙偲傪堄枴偟偰偄傑偡丅偳偺嵗昗偱傕巊偊傞曄姺幃偼傑偩媮傔傜傟偰偄側偄偺偱偡丅傕偟枹抦偺娭悢偵埾偹傜傟偰偄傞偼偢偺嵗昗曄姺偵(3)幃傪巊偊偽掕忢宯偐傜塣摦宯傊偺曄姺娭悢傪徣棯偡傞偙偲偵摍偟偔側傝傑偡丅憡懳惈棟榑偼昁偢偳偙偐偱娭悢傪尒棊偲偝側偄偲惉棫偟側偄棟榑偱偡丅(8)幃偺帪娫惉暘偵(3)幃偺懍搙偺岞幃傪嵦梡偟偰偄傞偺傕偦偺侾偮偱偡丅
僇儊懍搙堦掕偺朄懃
偁傞摿暿側僇儊偺曕偔懍搙偑扤偐傜尒偰傕堦掕偲壖掕偟傑偡丅乽僇儊懍搙堦掕偺朄懃乿偱偡丅偙偙偱偁側偨偼悽偺拞偺暔棟朄懃傪偙偺僇儊偵堷偒偢傜傟傞傛偆偵廋惓偟側偗傟偽側傜側偄偲寢榑偡傞偱偟傚偆偐丅偦傟偲傕僇儊偩偗偑屌桳偺朄懃傪帩偭偰偄傞偺偱懠偵塭嬁傪梌偊側偄偲寢榑偡傞偱偟傚偆偐丅擔忢惗妶偱偼僇儊偺摦偒側偳堄幆偟偰偄側偄偺偱屻幰偺摎傪偲傞偱偟傚偆丅偟偐偟丄僇儊偱側偔岝偲側傞偲慜幰偺摎傪偲偭偰偟傑偆偺偱偡丅憡懳惈棟榑偑惉棫偡傞偵偼僇儊偑暔棟朄懃傪巟攝偟偰偄傞偲寢榑偯偗傞偺偲摨偠峫偊傪摫擖偟側偗傟偽側傜側偄偺偱偡丅
傕偲傕偲乽岝懍搙晄曄偺尨棟乿偼乽岝乿埲奜偺暔棟朄懃偵塭嬁傪梌偊傞梫惪傪偟偰偄側偄偺偱丄岝懍搙傪堦掕偵偡傞偨傔偵帪娫傗嬻娫傪榗傔側偔偰傕傛偄偼偢偱偟偨丅偦偺徹嫆偵岝偩偗傪摿暿偵偡傟偽乽岝懍搙晄曄乿偺梫惪偼擄側偔僋儕傾偱偒傑偡丅傕偟丄懍搙偺扨埵偵岝昩傪嵦梡偡傟偽
們亖侾
娙扨偡偓傞傛偆偱偡偑尨棟偺梫惪傪枮偨偡偵偼偙傟偱廫暘偱偡丅偨偩偟丄偙偺幃偼懠偺幃偲偼姰慡偵愗傝棧偡偺偑忦審偵側傝傑偡丅岝偵娭偟偰偩偗悢妛宍懺偑堘偭偰偄傞偐傜偱偡丅偁傞偄偼娭悢昞帵偱丄
倖乮們乯
偲偟偰偍偒傑偡丅偙偺傛偆偵岝懍搙們偑傎偐偺偳偺悢抣偲傕寁嶼偱偒側偄傛偆偵偡傞偩偗偱乽岝懍搙晄曄偺尨棟乿偺梫惪偼傒偨偣傞偺偱偡丅堦曽丄榑暥偱偼們傪娭悢昞帵偣偢偵僈儕儗僀曄姺偵戙擖偟偰偄傑偡丅帪栤傪榗傔偰怴偟偄棟榑乮憡懳惈棟榑乯偺昁梫惈傪庡挘偡傞偨傔偱偡丅
嵟廔夝摎傊傓偗偰
憡懳惈棟榑偺楌巎偑巒傑傞捈慜偐傜倖乮們乯偼昿斏偵巊傢傟偰偒傑偟偨丅偟偐傕挿偄娫丄扤偵傕婥偯偐傟偢偵憡懳惈棟榑傪巟偊懕偗偰偒偨偺偱偡丅偦傠偦傠墢偺壓偺椡帩偪偵傕僗億僢僩儔僀僩傪偁偰偰偁偘傛偆偱偼側偄偱偡偐丅側偤憡懳惈棟榑偑悢妛揑偵娫堘偭偰偄傞偙偲偵婥偯偐側偄偺偐偼偙偺娭悢偺塀傟応強偵旈枾偑偁傞偺偱偡丅
偱偼乽岝懍搙晄曄偺尨棟乿偵婎偯偄偰丄師偺幙栤偵摎偊偰傒偰偔偩偝偄丅岝懍搙偼偄偐側傞嵗昗宯偱傕堦掕抣們偲偟傑偡丅
- 嘆懍搙侽丄偮傑傝惷巭偟偰偄傞娤應幰偵偲偭偰岝懍搙偼偄偔傜偱偡偐丠
- 嘇懍搙侾偱塣摦偟偰偄傞娤應幰偵偲偭偰岝懍搙偼偄偔傜偱偡偐丠
- 嘊懍搙円偱塣摦偟偰偄傞娤應幰偵偲偭偰岝懍搙偼偄偔傜偱偡偐丠
- 嘋懍搙們偱塣摦偟偰偄傞娤應幰偵偲偭偰岝懍搙偼偄偔傜偱偡偐丠
岝懍搙晄曄偱偼偡傋偰們偲摎偊傞偙偲偑偱偒傑偡丅偁側偨偼丠丂傗偼傝塣摦偟偰偄傞娤應幰偺懍搙偵娭學側偔岝懍搙偼們偱偡偐丠丂偦傟偧傟偺僨乕僞丄侽傗侾丄円傗們偼偳偆側偭偨偺偱偟傚偆偐丅偦傟傜傪偡傋偰柍帇偟傑偣傫偱偟偨偐丠
偙偙偱怴偨側塣摦偺朄懃傪婰弎偟傛偆偲巚偭偨傜丄崱傑偱巊偭偰偄偨僈儕儗僀曄姺偲偺堘偄傪柧妋偵偟丄峴偭偨悢妛揑嶌嬈偼惓妋偵婰弎偟側偗傟偽側傜側偄偼偢偱偡丅偨偲偊偦傟偑埫嶼偱偒傞傎偳娙扨側寁嶼偱偁偭偰傕偱偡丅僈儕儗僀曄姺偱偼娤應幰偺懍搙円偼嶍彍偝傟傑偣傫偱偟偨偑丄岝懍搙晄曄偺尨棟偱偼堘偄傑偡丅
倖乮們乯偑俀偮偺僨乕僞偺偆偪娤應幰偺懍搙円傪嶍彍偟偰們偩偗傪嵦梡偡傞娭悢偩偲偄偆偙偲傪峫椂偡傟偽僨乕僞偵偼円傕擖傝傑偡丅
倖乮們丄円乯
偲偡傞偺偑傛傝惓妋側昞婰偱偟傚偆丅偙偆偟偰偼偠傔偰丄乽娤應幰偺懍搙偵娭學側偔岝懍搙傪們偵偡傞乿偙偲偑壜擻側偺偱偡丅偲偙傠偑憡懳惈棟榑偵偼丄偙偺傛偆側娭悢偼搊梘偟傑偣傫丅搊応偟偰偼崲傞偺偱偡丅
娭悢倖乮們丄円乯偵偼丄師偺傛偆側悢妛揑寚娮偑偲傕側偄憡懳惈棟榑偺妀傪宍惉偟偰偄傑偡丅傕偆堦搙幙栤偵摎偊偰偔偩偝偄丅岝懍搙晄曄偱偺岝懍搙傪摎偊傞偲偒丄偁側偨偼埫嶼傪偟傑偣傫偱偟偨偐丠
憡懳惈棟榑傪棟夝乮丠乯偟偰偄傞恖偼昁偢偟偰偄傞偼偢偱偡丅岝懍搙俠偼扤偐傜尒偰傕僈儕儗僀曄姺偝傟傑偡傛偲尵傢傟傟偽幃傪彂偄偰偄偨偺偵丄扤偐傜尒偰傕丅堦掕偱偡傛偲尵傢傟傞偲偮偄偮偄埫嶼傪偟偰偟傑偆偺偱偡丄摎偼們偩偲丅
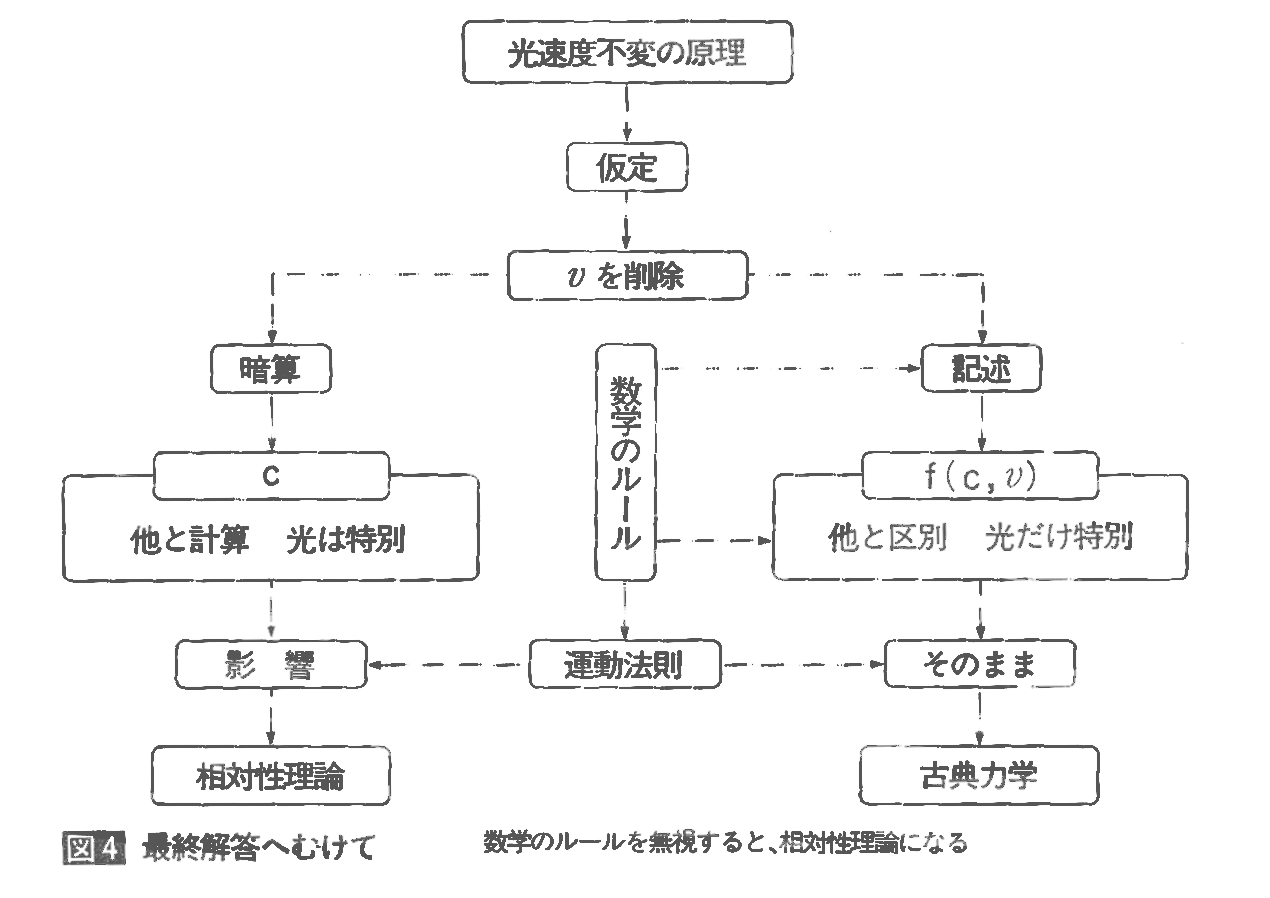
偙偺埫嶼偙偦俋侽擭偵傢偨偭偰壦嬻偺棟榑傪巟偊偰偒偨嵟戝偺乽僔儖僶乕僴儞儅乕乿丄憡懳惈棟榑偺嵟廔夝摎偲傕尵偊傞傎偳廳梫側傕偺偱偡丅柍忦審偵庴偗擖傟偞傞傪偊側偐偭偨婎杮揑側愝掕偺側偐偵敪尒傪晄壜擻偵偡傞僩儕僢僋偑塀偝傟偰偄偨偺偱偡丅憡懳惈棟榑傪棟夝偡傞偵偼傑偢嵟弶偵偙偺僩儕僢僋偵傂偭偐偐傜側偗傟偽側傝傑偣傫偱偟偨丅挿偄娫丄恖乆傪擸傑偣偰偒偨憡懳惈棟榑偺娫堘偄偑偨偭偨侾峴偱愢柧偱偒傞偺偱偡丅
乽埫嶼偵巊偭偨娭悢偑婰擖偝傟偰偄側偄乿
摢偺拞偵抲偒朰傟偨娭悢倖乮們丄円乯偼妋幚偵憡懳惈棟榑傪曵夡偝偣偰偟傑偄傑偡丅娭悢偺婰擖偱幃偺揥奐偑偱偒側偔側傞埲慜偵棟榑偺懚嵼棟桼偦偺傕偺偑側偔側偭偰偟傑偆偐傜偱偡丅偙傟偵偝偊婥偯偄偰偄傟偽俀侽悽婭偺朿戝側楯椡偑柍懯偵側傜偢偵偡傫偩偙偲偱偟傚偆丅
巹偺庡挘偡傞敪尒偼乽娭悢偺妵屖傗扨埵傪徣棯偟偰昞婰偡傞暔棟妛偺廗姷傪岆夝偟偨傕偺偩乿偲偺斀榑傕峫偊傜傟傑偡丅偟偐偟愱栧壠偺塀傟偨僲僂僴僂偲偟偰巊傢傟偰偄傞徣棯婰朄偑廳戝側儈僗傪惗偠偰偄傞偺偱偁傟偽丄偙傟偼栤戣偱偡丅巹偼偦傟傪巜揈偟偨傢偗偱偡丅嶲峫偺偨傔姫枛偵傾僀儞僔儏僞僀儞偺榑暥傪丄偦偺傑傑偺宍偱宖嵹偟偰偍偒傑偡丅
儅僀働儖僜儞丒儌乕儗乕偺幚尡偵偮偄偰
憡懳惈棟榑偑娫堘偭偰偄傞偙偲傪愢柧偟偰傕乽憡懳惈棟榑偼幚尡偱徹柧偝傟偨乿偲丄斀榑偝傟傞幚尡偺侾偮偵儅僀働儖僜儞丒儌乕儗乕偺幚尡偑偁傝傑偡丅偙偺幚尡偼乿1887擭丄憡懳惈棟榑偺敪昞埲慜偵峴傢傟傑偟偨偑丄屆揟椡妛偺柕弬偲岝懍搙晄曄偺昁梫惈傪傾僺乕儖偡傞偵偼嵟揔側帠椺偱丄昁偢偲偄偭偰偄偄傎偳堷梡偝傟偰偄傑偡丅
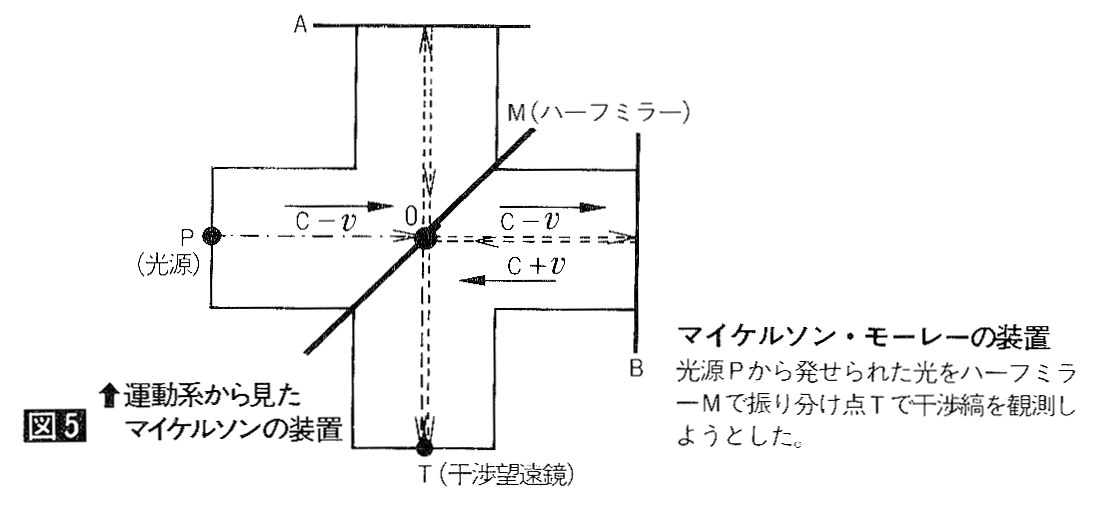
偦偺憰抲偼侾偮偺岝尮偐傜敪偣傜傟偨岝傪僴乕僼儈儔乕偵傛偭偰俀偮偺岝楬偵暘棧偟丄悢夞偺斀幩偺偺偪偵嵞傃堦揰偵廤傔傞傕偺偱偟偨乮恾5乯丅偦偟偰丄憰抲慡懱傪夞揮偝偣偰丄姳徛幦偺曄壔偐傜岝楬挿偺堘偄傪尒弌偦偆偲偟偨偺偱偡丅
傕偟丄岝懍搙晄曄偱側偄側傜偽丄抧媴偺岞揮偵傛傞曄壔傪専弌偱偒傞偼偢偱偟偨偑丄娤應偺寢壥丄俀偮偺岝偺姳徛幦偵曄壔偼擣傔傜傟傑偣傫偱偟偨丅偙傟偑崱偱傕岝懍搙晄曄偺棫徹幚尡偲側偭偰偄傞偺偱偡丅
偄偔傜憡懳惈棟榑偺岆傝傪徹柧偟傛偆偲偟偰傕偡偱偵岝懍搙晄曄偺尨棟偑幚徹偝傟偨偲巚傢傟偰偄傞偺偱偡丅偟偐偟丄幚尡傪怲廳偵専徹偡傟偽丄堦斒偵抦傜傟偰偄傞寢榑偲偼慡偔斀懳偺寢壥偑憰抲偺尨棟偵傕塀偝傟偰偄傞偙偲偑傢偐傝傑偡丅偮傑傝丄憡懳惈棟榑偼侾侽侽擭埲忋傕慜偵斲掕偝傟偰偄偨偺偱偡丅
岝懍搙晄曄偼斲掕偝傟偰偄偨
傑偢丄偙偺憰抲偱岝懍搙晄曄偺尨棟傪専徹偟偰傒傑偡丅堦斒揑偵偙偺専徹偼塣摦宯乮抧媴忋偺娤應幰偺宯乯偺傒偱峴傢傟偰偒傑偟偨偑丄掕忢宯偐傜傒偨揰俿偵偼姳徛幦偑娤應偝傟傞偙偲偑梊憐偝傟傑偡丅憡懳惈棟榑偱偼摨帪惈偺奣擮偼斲掕偝傟偰偄傞偐傜偱偡丅偙偺帪揰偱岝懍搙晄曄偺尨棟偼柕弬偟傑偡偑丄暿偺傾僾儘乕僠傪偟偰傒傑偟傚偆丅
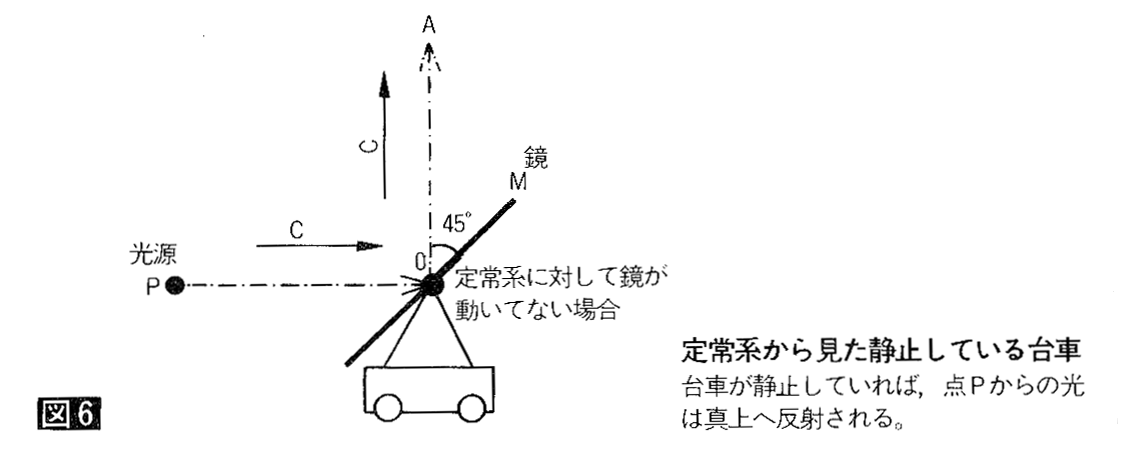
恾俇偺傛偆偵嬀偑愝抲偝傟偨戜幵傪憐掕偟傑偡丅巻柺嵍偐傜岝偑敪幩偝傟丄嬀偵係俆搙偺擖幩妏偱傇偮偐傝丄巻柺忋曽傊斀幩偝傟偨偲偟傑偡丅戜幵偑巭傑偭偰偄傟偽丄佢俹俷俙偼俋侽搙偱偡丅傕偟丄戜幵偲娤應幰偑倶幉曽岦傊懍搙円偱塣摦偟偰偄偰偄傟偽丄佢俹俷俙丩偼俋侽搙傛傝彫偝偔側偭偨傛偆偵尒偊傞偱偟傚偆丅乮恾俈乯
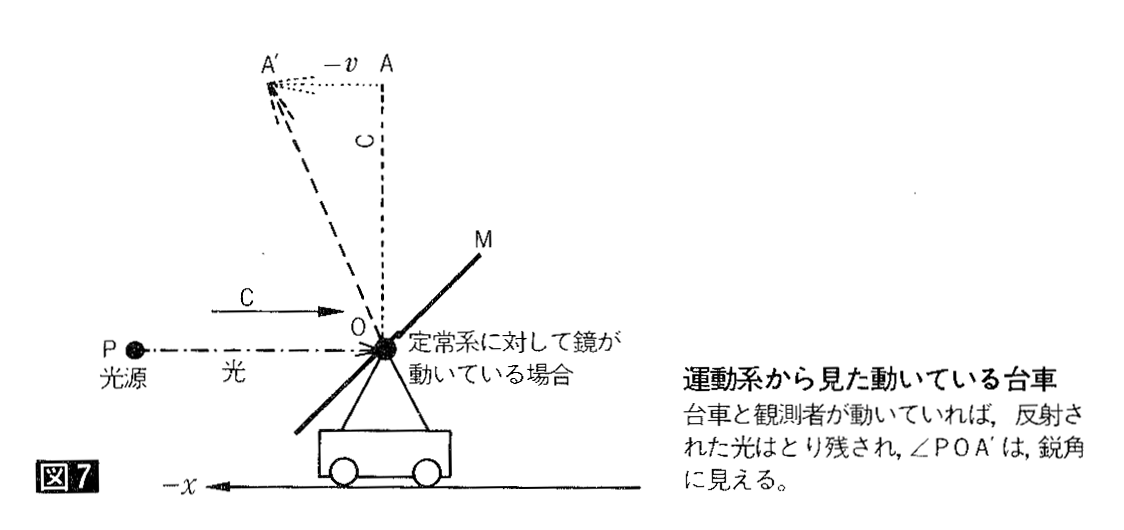
偙偙偱岝懍搙晄曄偵廬偊偽慄暘俷俙丩偼慄暘俷俙偲摨偟挿偝偱側偗傟偽側傜側偄偺偱丄嬀偺妏搙傪曄偊偰俀杮偺慄暘偑摍偟偔側傞傛偆挷惍偟偰傒傑偡丅乮恾俉乯
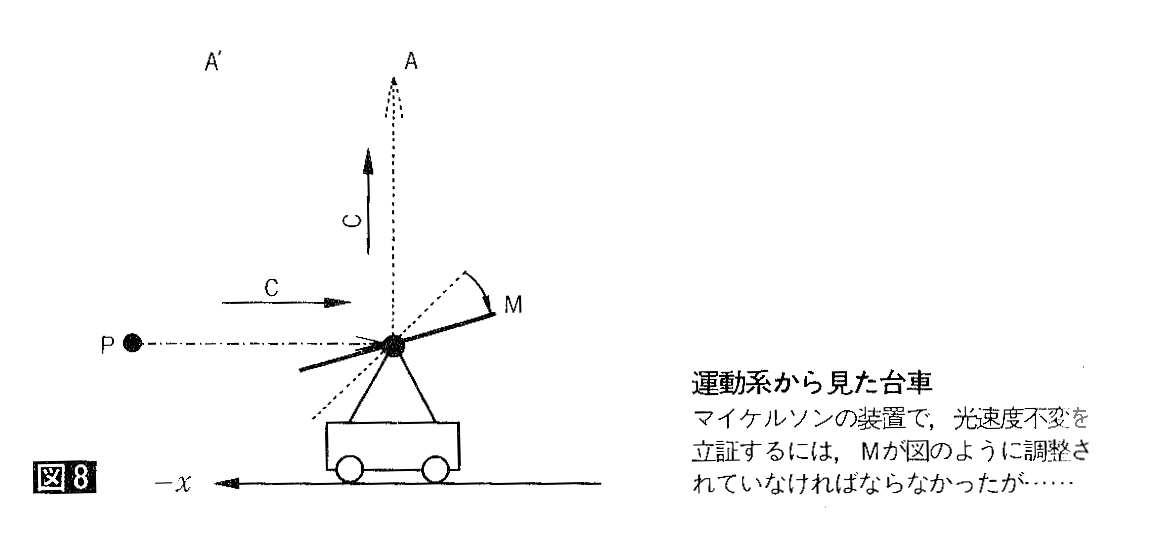
岝懍搙晄曄傪棫徹偟偨儅僀働儖僜儞丒儌乕儗乕偺憰抲偱傕摨偠傛偆偵僴乕僼儈儔乕俵偼挷惍偝傟偰偄偨偺偱偟傚偆偐丅幚尡憰抲傪偳偺曽岦傊岦偗偰傕曄壔偑娤應偝傟側偐偭偨偲偡傟偽丄僴乕僼儈儔乕俵偼岝慄偵懳偟偰惓妋偵係俆搙偺妏搙傪曐偭偰偄偨偲寢榑偣偞傞傪偊傑偣傫丅偦偆偱側偗傟偽丄岝慄俙丄俛偼暯峴傪堐帩偱偒偢丄揰俿偱姳徛幦偵曄壔傪婲偙偟偰偟傑偆偐傜偱偡丅偮傑傝丄慄暘俷俙丩偲慄暘俷俙偼摨偠挿偝偱偼側偐偭偨偙偲偵側傝傑偡丅岝懍搙晄曄偺壖愢偼儅僀働儖僜儞丒儌乕儗乕偺幚尡偵傛偭偰偡偱偵斲掕偝傟偰偄偨偲偄偆偙偲偱偡丅
婏柇側岝
偨偟偐偵儅僀働儖僜儞丒儌乕儗乕偺幚尡寢壥偼屆揟椡妛傪斲掕偟偰偄傑偡丅偟偐偟丄偦偺専徹偵梡偄傜傟偰偄傞岝偼屆揟椡妛偺岝偲偼傑偭偨偔堘偭偨婏柇側岝偱偡丅傑偢偙偺岝偵偮偄偰擣幆偟偰偍偄偨曽偑傛偝偦偆偱偡丅
乵壖憐幚尡侾乶
帪懍侾侽侽倠倣偱憱偭偰偄傞楍幵偵娤應幰俙偑忔偭偰偄傑偡丅楍幵偺奜懁偵偼娤應幰偺尒偊傞埵抲偵忎晇側暻偑愝抲偟偰偁傝丄俙偼楍幵傪捛偄墇偦偆偲偡傞暔懱偑暻偵徴撍偡傞弖娫傪娤應偡傞偙偲偑偱偒傞偲偟傑偡丅乮嶌恾俋乯
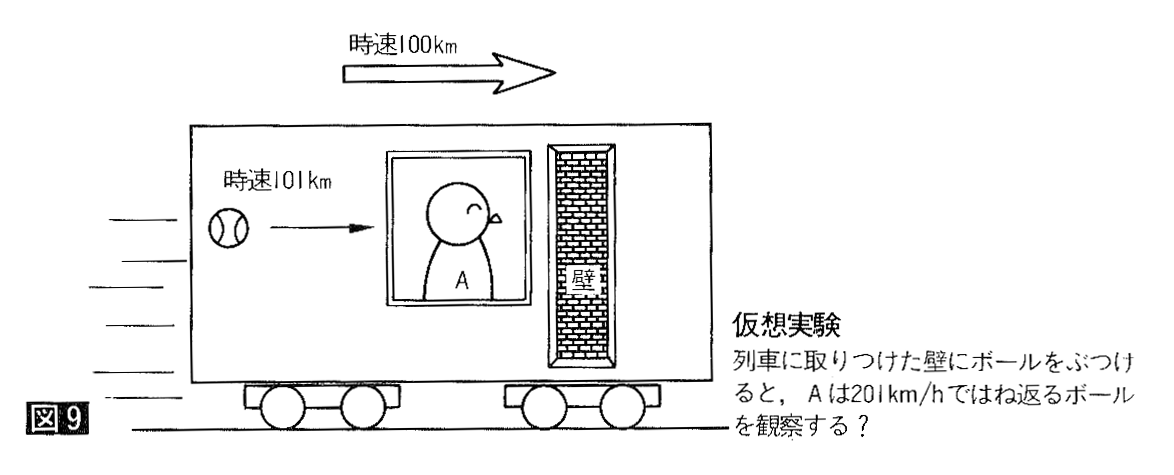
偄傑丄帪懍侾侽侾倠倣偱姰慡抏惈懱偺儃乕儖偑楍幵傪捛偄墇偦偆偲偟偰偙偺暻偵傇偮偐傝傑偟偨丅娤應幰俙偼偳偺傛偆側尰徾傪娤應偟偨偱偟傚偆偐丅偨偩偟丄嬻婥掞峈傗廳椡偼柍帇偟傑偡丅
- 峫嶡嘆
- 儃乕儖偑帪懍侾倠倣偱暻偵徴撍偟偨偺偪丄帪懍侾倠倣偱屻戅偟偰偄偔偲偙傠傪娤應偟偨丅
- 寁嶼偼丄偦傟偧傟丄
- 侾侽侾亅侾侽侽亖侾
- 侾侽侽亅侾侽侾亖亅侾
- 峫嶡嘇
- 儃乕儖偑帪懍侾倠倣偱暻偵徴撍偟偨偺偪丄帪懍俀侽侾倠倣偱屻戅偡傞偲偙傠傪娤應偟偨丅
- 寁嶼偼丄
- 侾侽侾亅侾侽侽亖侾
- 侾侽侾亄侾侽侽亖俀侽侾
峫嶡嘆偼帺慠偵憐憸偱偒傑偡偑丄峫嶡嘇偼偐側傝柍棟偑偁傝傑偡丅側偵偟傠丄帪懍侾倠倣偺儃乕儖偑暻偵徴撍偟偨捈屻丄帪懍俀侽侾倠倣偵壛懍偝傟偰偟傑偆偺偱偡丅傕偟丄尰幚偵偙偺傛偆側尰徾偑婲偒傞偲偡傟偽丄楍幵撪傊偺儃乕儖偺帩偪崬傒偼嬛巭偝傟偰偄傞偱偟傚偆丅傑偨丄楍幵偺慜晹傊堏摦偡傞帪偵傢偢偐偱傕懱偑傇偮偐傞偲屻晹傊抏偒旘偽偝傟傑偡丅偙偆側傞偲楍幵偵忔傞偺傕柦偑偗偱偡丅
幚偼儅僀働儖僜儞丒儌乕儗乕偺幚尡偱丄屆揟椡妛偺専徹偵巊傢傟偰偒偨偺偼峫嶡嘇偺幃偱偡丅懍搙乮們亅円乯偱徴撍偟偨岝偑乮們亄円乯偵壛懍偝傟偰偄傞偆偊丄掕忢宯偐傜偵尒傞偲斀幩偺慜屻偲傕懍搙們偱偡丅屻戅偟偰偄傞嬀偵斀幩偟偨岝偼僪僢僾儔乕岠壥偝偊婲偙偟傑偣傫丅偙傟偼屆揟椡妛偺岝偲偼慡偔堎幙偺岝偱丄乽屆揟暔棟妛斲掕梡偺岝乿側偺偱偡丅
屆揟椡妛偵廬偊偽丄塣摦偡傞娤應幰偼丄懍搙乮們亅円乯偺岝偑嬀偵斀幩偟偨屻丄懍搙乮亅們亄円乯偵曄壔偡傞偺傪尒傞偼偢偱偡丅
屆揟椡妛偺専徹
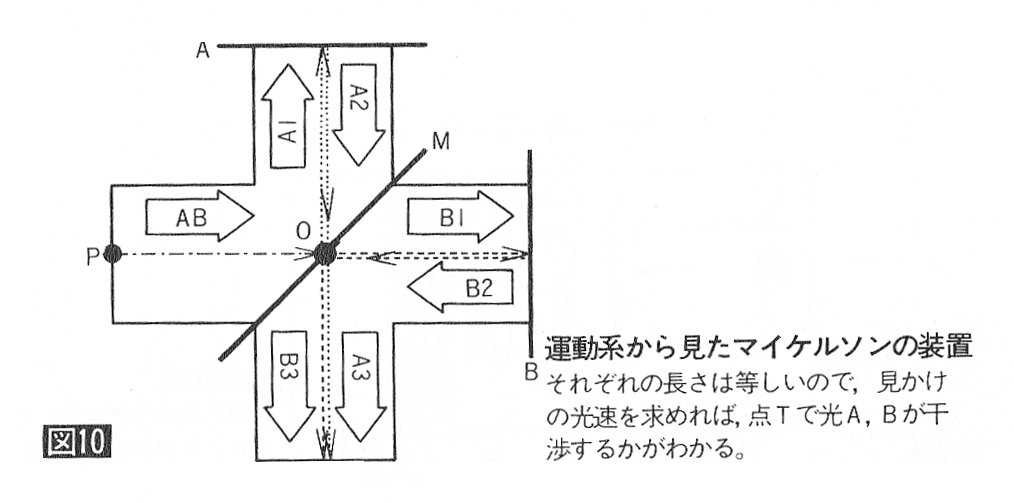
偝偰丄偦傟偱偼儅僀働儖僜儞丒儌乕儗乕偺幚尡傪屆揟椡妛偱愢柧偟傑偟傚偆丅恾侾侽偼憰抲偺棯恾偱丄俙丄俛偦傟偧傟偺懍搙偼偄傑偺偲偙傠枹抦偱偡丅偙偺懍搙傪侾偮侾偮妋幚偵媮傔偰偄偔偙偲偱栤戣傪夝寛偟偰偄偒傑偡丅
愭偼偳偺寢壥偐傜俙俛丄俛侾偑乮們亅円乯丄俛俀偵偼乮亅們亄円乯偑擖傝傑偡丅偨偩偟丄俛俀偼晞崋傪偦傠偊偰乮們亅円乯偵偟傑偡丅嵞傃恾俇傪尒偰丄岝俙偺懍搙偵偮偄偰峫嶡偟偰傒傑偟傚偆丅戜幵偼懍搙円偱塣摦偟偰偄傑偡丅墦偞偐偭偰峴偔暻偵儃乕儖傪傇偮偗傞偲丄儃乕儖偺懍搙偼尭彮偟傑偡丅偟偨偑偭偰丄掕忢宯偵偄傞娤應幰偼嬀偵岝偑徴撍偟偨屻丄岝偺懍搙偑尭彮偡傞偺傪尒傞偱偟傚偆丅
儈儔乕俵偼係俆搙側偺偱丄倶幉曽岦偵円偩偗堏摦偟偰傕丄倷幉曽岦偵傕円堏摦偟偨偙偲偵側傝傑偡丅倶惉暘丄倷惉暘偵暘夝偟偰峫偊偨傎偆偑偄偄傛偆偱偡丅偙偺揰偵婥傪偮偗偰恾俇傪廋惓偡傞偲丄恾侾侾偵側傝傑偡丅偝傜偵偙傟傪懍搙円偱塣摦偡傞娤應幰偐傜尒偨儅僀働儖僜儞丒儌乕儗乕偺専徹恾偵揔梡偟偨偺偑恾侾俀偱偡丅偄偢傟傕懍搙傪慄暘偺挿偝偱昞偟偨傕偺偱偡丅偙偺恾偐傜恾俋偺俙侾偑乮們亅円乯偩偲傢偐傝傑偡丅儈儔乕倎偵偮偄偰偼倷惉暘偵曄壔偑側偄偺偱丄岝偼懍搙乮們亅円乯偺傑傑斀幩偝傟揰俿偵払偟傑偡丅偟偨偑偭偰丄俙俀丄俙俁偵傕乮們亅円乯偑擖傝傑偡丅
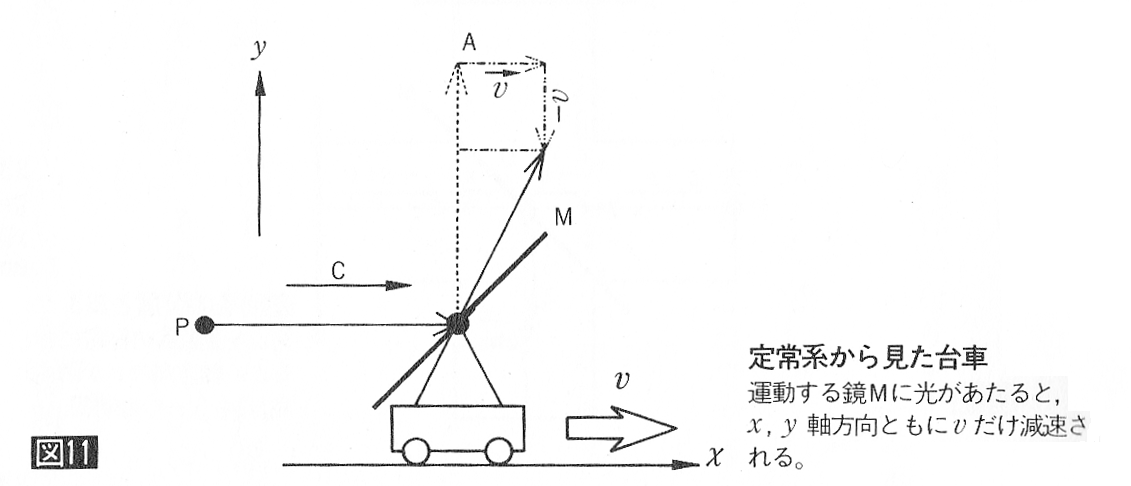
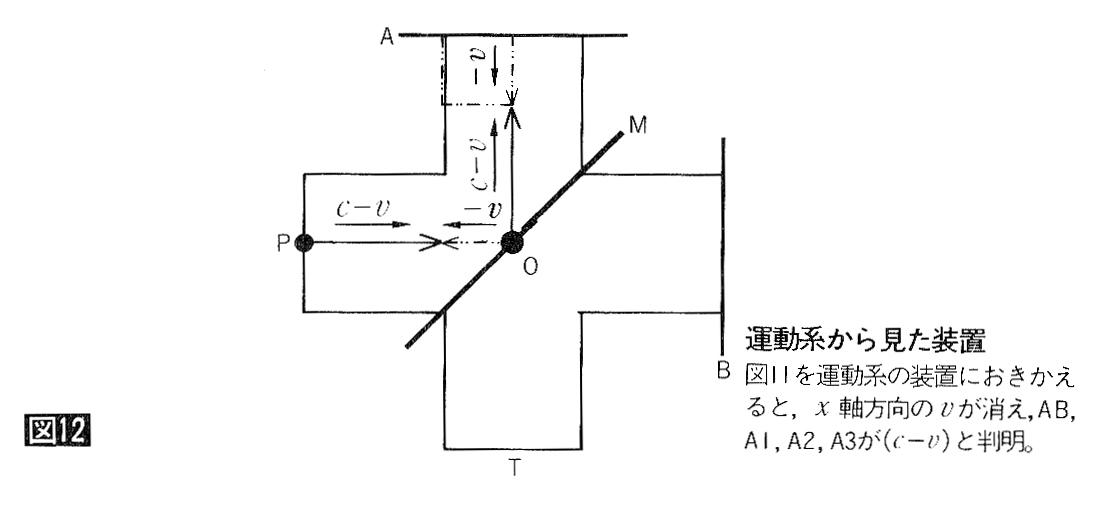
巆傞偼俛俁偩偗偱偡丅塣摦宯偐傜傒傞偲丄俛俀偼乮們亅円乯偱偡丅掕忢宯偵曄姺偡傞偨傔円傪壛偊傑偡丅偟偐偟丄俛俀偼晞崋傪曄偊偰偄偨偺偱丄堦扷栠偟傑偡丅
乮亅們亄円乯亄円亖亅們亄俀円
嵞傃曽岦傪偦傠偊傟偽乮們亅俀円乯偱偡丅媡岦偒偺懍搙偩偐傜抶偔尒偊傞偺偱偡丅
偙傟傪嬀偑係俆搙偱偁傞偙偲丄懍搙円偱嬤偯偄偰偔傞偙偲傪峫椂偟偰嶌恾偡傞偲丄恾侾俁偵側傝傑偡丅偙傟傪塣摦宯偐傜尒偨恾偵廋惓偟偨偺偑恾侾係偱偡丅寢嬊俛俁傕乮們亅円乯偺傛偆偱偡丅
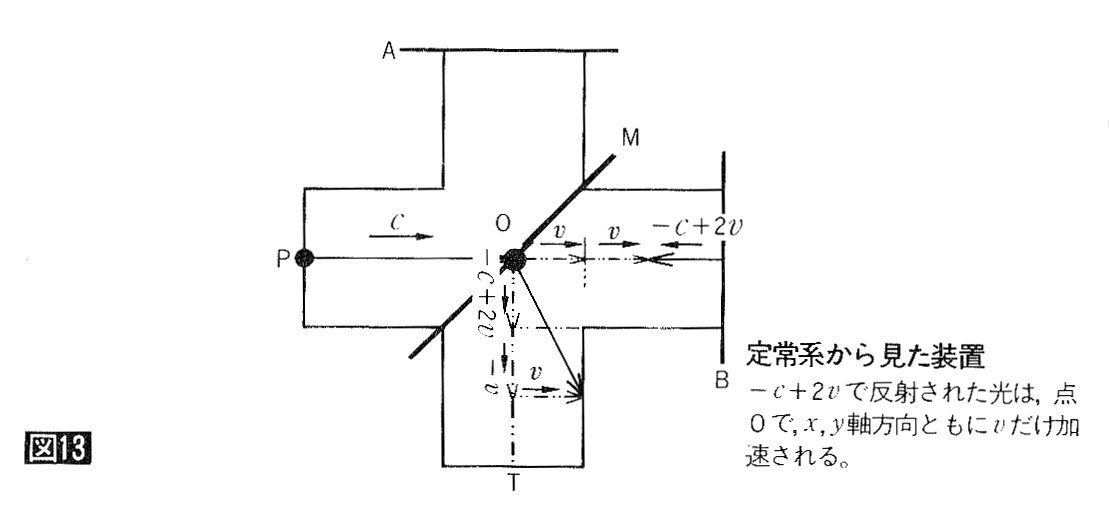
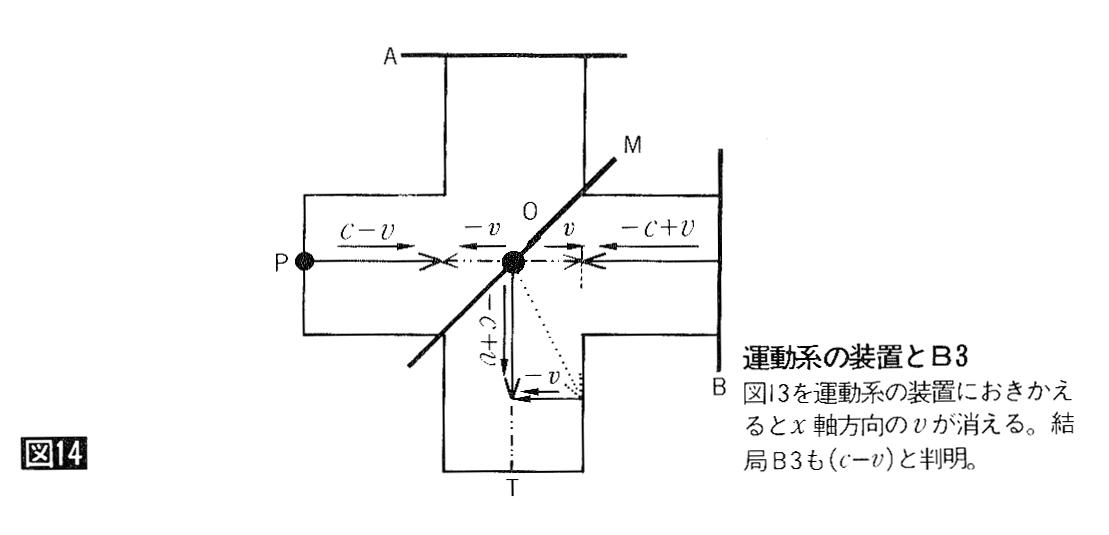
佢俹俷俙丩丂佢俛俷俿偼捈妏側偺偱丄岝楬挿俙丄俛偼慡偔摨偠偱偡丅懍搙傕偡傋偰乮們亅円乯偱偟偨丅偟偨偑偭偰丄岝俙丄俛偼摨帪偵揰俿傊摓払偟丄姳徛幦偺曄壔偼娤應偝傟側偄偙偲偵側傝傑偡丅偙傟偱儅僀働儖僜儞丒儌乕儗乕偺幚尡傪屆揟椡妛偩偗偱愢柧偱偒傑偟偨丅
偁傞偄偼傕偭偲摏扨偵丄塣摦宯偐傜尒偨懍搙俙俛偑乮們亅円乯側傜塣摦検曐懚偺朄懃偐傜偡傋偰偑乮們亅円乯偲寢榑偟偰傕偄偄偱偟傚偆丅
彜嬈壔偟偨暔棟妛偵桬婥偁傞屻戅偼偱偝傞偐
尰戙暔棟妛偑憡懳惈棟榑傪昁梫偲偟偨傛偆偵棟榑偲幚尡偺憡堘偼惓偟偄棟榑傪梫媮偟偰偄傞傛偆偵巚偊傑偡丅懡偔偺棟榑偑弌偰偼徚偊偰峴偔拞偱丄埨堈偵屆揟椡妛傪曻婞偡傞偺偱偼側偔丄偦偺拞偵乽僔儖僶乕僴儞儅乕乿傪扵偡偺偼崻杮揑側夝寛曽朄偺侾偮偩偲巚偄傑偡丅
傕偟丄撠傪偍偩偰偰栘偵搊傜偣傞尋媶偵惻嬥偑楺旓偝傟偰偄偨傜扤傕偑媈栤傪書偔偱偟傚偆丅嫄妟偺帒嬥偱寶愝偝傟偨撠幧偱偼枅擔偺傛偆偵尋媶幰払偑恀寱偵撠傪偼傔懕偗丄栘偵搊傞弖娫傪崱偐崱偐偲懸偪傢傃偰偄傞偺偱偡丅悢擭偨偭偰壗偺惉壥傕摼傜傟側偄偲乽傕偭偲帒嬥傪偐偗傟偽撠傪偍偩偰傞曽朄偑尒偮偐傞偐傕偟傟側偄乿偲偦傟傜偟偄偙偲傪尵偄傑偡丅栘偵搊傞偐側偳傕偆偳偆偱傕偄偄偺偱偡丅扤偐偑偦傟偑偨偩偺偙偲傢偞偩偲嫵偊偰傕懕偗傞偱偟傚偆丅
愱栧壠偑棟榑偺惓偟偝傪愰揱偡傞側偐偱丄岞暯側栚傪懸偭偨恖払偼岆偭偨棟榑傪傕偆堦搙専徹偡傞廳梫惈傪慽偊偰偄傑偡丅憡懳惈棟榑偼暔棟妛偱偼側偔悢妛僩儕僢僋偱偡傛偲嫵偊傜傟偰傕丄傢偢偐侾侽暘偱曵傟傞棟榑偵挊柤側愭惗曽偑偟偑傒偮偄偰偄傞巔偼偁傑傝偵傕妸宮偱偡丅憡懳惈棟榑傪彞偊偰偄側偑傜棟榑偺朻摢傪専徹偟傛偆偲傕偟側偄偺偼側偤偱偟傚偆偐丅
偙偺復偱偼丄憡懳榑偺杮偝偊偁傟偽娙扨側悢妛偱岆傝傪専徹偱偒傞偙偲傪帵偟傑偟偨丅懡偔偺栤戣傪堷偒婲偙偟偰偄傞憡懳惈棟榑傪乽怣偠傞乿偐偦傟偲傕乽専徹乿偡傞偐偼屄恖偺椣棟偵偐偐偭偰偄傞偺偱偡丅戝愗側偺偼侾恖侾恖偑傛偔妋擣偟偰丄岆偭偨棟榑傪塋撣傒偵偟側偄偙偲偱偡丅偼偨偟偰彜嬈壔偟偨尰戙暔棟妛偵傕桬婥偁傞屻戅偑偱偒傞偺偱偟傚偆偐丅揤嵥偺弌偟偨僷僘儖偺杮摉偺夝摎偼偦偙偵塀偝傟偰偄傞傛偆偱偡丅
侾擔偱傕憗偄夝寛傪婅偄側偑傜偙偺榑峫傪廔傢傝傑偡丅
