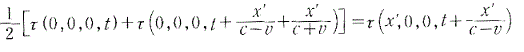妄想？　アクシオンこと木下篤哉氏の批判文の場合

　　　　　　以下、『「相対論」はやはり間違っていた』はやはり間違っていたより引用、抜粋

相対論を打ち砕くシルバーハンマー：日高　守氏
［シルバーハンマーとは何か］

著者によると、シルバーハンマーというのは、理論が構築された後に発見される見落とされた関数の事だそうです。要するに理論構築の土台となった部分に単純なミスが見付かると、親亀コケたら皆こけたというように総崩れになるという事のようです。

まあ、確かにそうです。逆説的ではありますが、この本に書かれている“相対論は間違い”とする説は、著者の言うシルバーハンマーによって崩れているのですから（＋実験事実の誤認もあります）。

おそらく最後まで反論材料を見つけられなかったのでしょう。反証となるシルバーハンマーは１つも出てきません。創作批判した内容が相対論と矛盾することにも気づいていないようです。

［二〇世紀最大の発見］

この節で著者は歴史的な式E=Mc2が一般に知られているような重要な意味を全く持っていないとし、それを説明しています。実は、私個人も歴史的な意味という事から考えれば、・・・

本書を書いた著者達は、一人を除いて異口同音に「相対論はアインシュタイン一人がデッチあげた」という主張でありますので、・・・

・・・歴史的背景省略・・・

・・・仮想実験の説明と考察省略・・・

M'-M = E/c²　今回増えた質量分はまさに、M'-Mであるから、
増加分(M'-M)を新たにMとすれば、E = Mc²とできる。

・・・省略・・・

・・・なおかつ速度が変化していないという前提では、運動量保存則を満たすためには、質量が変化したと考えるのが一番妥当です。

・・・省略・・・

著者の指摘は、この論文には観測や実験での事実の記載が一切なく、仮想実験だけで書いてあるので間違っているというものです。

もちろん、「相対論はアインシュタイン一人がデッチあげた」と主張した箇所はありません。こういうのはデッチあげです。ただ、マイケルソンやローレンツが二ュートン力学の考えで犯した誤りがアインシュタインの論文に複数含まれていることから、アインシュタインが盗作した可能性は非常に高いでしょう。

E=Mc²の論文については、

という単純明快な指摘をしているだけです。要は仮想実験を正しく式に表現できているかを検証すればいいとわかります。歴史的背景と式の評価の妥当性については、式の正当性を立証してから実施するべき内容です。

指摘の中で単位の話には相当数の反論、批判がありました。しかしそれらすべて、一般化や組立単位の本質を考慮していないものでした。E=Mc²の導出で必ず出てくる一般化を軽く見ているのが、反対意見の盲点です。

このまま式に単位を設定して評価するのが通例となっています。一般化によって、初期設定より確実に物理情報が減少しているにもかかわらず、不明な変換係数が導出できてしまうのは、ちょっと考えればおかしいと気づきます。

一般化してもなお量的評価をしたいなら、初期設定の段階で未知の係数を取り入れ、それを求めるだけです。そもそもアインシュタインは、エネルギーE、質量M、に「量」の情報を設定したのか？　という話です。

E=Mc²の論文には「量」を表現する工程が抜けています。E=Mc²が偉大な式だと思っている人は、論文のはじめから未知の係数βを導入してみいるといいでしょう。E = Mc²　は完成するあてのない理論式だとわかるはずです。

仮に目の前で確実にエネルギーが質量に変換されたとしても、E = Mc²とは関係ない現象です。本文で「Ｅ＝Ｍｃ²に従った物理現象などはこの世に存在しない」と言っているのは、誤謬で出来ている架空の式だからです。

このように仮想実験は広い意味で予想、予測を含み、これを否定してしまうと物理学は応用できない学問になってしまいます。仮想実験だけで書いた論文は間違いだと主張していないことはわかると思います。

本文の文章で書ききれなかった内容は図１に名残を残しています。それには運動量保存の法則の適用が誤っているために係数「c²」が発生していることなども書き入れてあります。その他十数項目の指摘は「Ｅ＝Ｍc²は架空の式」にあります。興味のある人は謎解きに挑戦してみてはいかがでしょう。

［それでも相対論？］

日高氏は数式の省略を許さない人で、見れば分かるから略していいだろうという部分があると間違いとして指摘します。この節では、著者のこの姿勢が露になります。例えば時間τを別の時間tと関連づけるとしてτ(0,0,0,t)と書いた後、それの時間微分として、

∂τ/∂t

としてある部分に反論します。τ(0,0,0,t)の時間微分ならば、

∂τ(0,0,0,t)/∂t

とすべきであろうと(^_^;)。その通りです。それはもちろんそうなんですが…なんと言うか、こういう突っ込みをされると凄く疲れそう。

アインシュタインは論文の目的を「方程式の組を見いだすことである」と明言しています。しかし、使われた解法は関数でなく係数を求める方法です。関数τも同じ論文中で時刻や時間、係数に変化します。つまり、相対論を認めてしまう人は関数と係数の違いを認識できていないということです。

関数の省略型を延長したものを係数として展開すると、未知の関数が求められたように錯覚します。これを関数の括弧の数に着目して「(9)式以降の高等式を検証しなくてもよい」としました。検証も反論も簡単にできる内容です。

と主張しているのだから、微分その他の演算も使えないということです。しかし、「見れば分かるから」と確認もしない人は、式を勝手に創作する傾向があります。

木下氏は著者が ∂τ(0,0,0,t)/∂t とすべきだと主張していると述べていますが、このような式を主張することはありません。

各パラメータをどう処理したかは、すでにτで代替され方程式が含まれているので、処理前のｔ との変化比は総合的な係数となります。関数の本体ではないのです。ちなみに、この結果を関数の導出にフィードバックする相対論では、関数が余計にカウントされた影響で解は平方根の形をとります。

x,y,z,t に入れるべきパラメータを決定している法則、それが未知の関数が従属している基本の関数です。パラメータ（c-v）(c+v）を入れたなら、ニュートン力学に従属することがおのずと決定されます。相対論の導出方法が誤っているのは、式の形を見れば分かります。

話が前後しますが、著者は冒頭の一節にこのような文を書いています。

そういう私は相対性理論を疑ったことが一度もありません。まったく理解できなかったのです。なぜ間違った式を使っているのか。なぜ物理学者までもが小学生でもわかる数学トリックに騙されてしまうのでしょうか。

…多分著者のような性格だと、相対論だけでなく、他の物理理論も全く先に進めず、「何故間違った式を…」と連発する事になると思いますが如何でしょうか？ これは数学屋さんが見て、物理屋さんの使う数学がいい加減なので、少々気を悪くしているというレベルの話ではありませんよね。

相対性理論を一度も疑うことなしに誤りに気付いたというのは誇張のない事実です。これは「アインシュタインのトリックがわかった！」の書籍版でも紹介していますが、

なぜピタゴラスの定理が最終定理の例外になっているのか、それを解明することで最終定理を証明できないかと考えました。しかし悪戦苦闘の末に決まって毎回同じような式が現れます。この式は座標変換の欠陥で発生する人為的な誤謬です。

この見慣れた式、見慣れた特徴、見慣れた見落としが、始めて読んだ相対性理論の入門書でローレンツ変換と呼ばれていました。数学で避けるべき誤謬が、理論物理学では基本法則に祭り上げられているのは、滑稽以外の何物でもありません。

というわけです。

誤った座標変換でローレンツ変換が現れる事実を少しでも知っていたなら、現代物理学のあまりに初歩的な誤りに「なぜ？」と疑問が湧くはずです。しかし、相対論に異議を唱えるのは疑似科学扱いするべきだ、という物理学者もいます。相対性理論の誤りが議論されないのは、正しいからではなく、疑似科学者扱いされたくないからでしょう。

ローレンツ変換の発生原因が誤謬とわかれば、ニュートン力学や電磁気学の応用段階で座標変換の見落としを修正するだけです。相対論の実証実験もローレンツ変換をなぞっているだけなので、時空を歪める理論は必要ありません。

妄想だらけで批判する疑似科学もなくなるでしょう。

次に、光が時刻τ0の時にX軸に沿ってx'まで進み、τ₁の時に反射し、τ₂で原点に戻った時の事を考えます。ここで、装置と共に動く慣性系からみれば、

1/2（τ₀+τ₂）=τ₁

であるとできます。何しろ装置と一緒に運動していると見る系では、光源も反射板も止まっているのですから。

そして、今度は装置を動いていると見る系…すなわち観測者に対して装置はvの速度を持って動いていて、光源も反射板も動いているとします。その観測者のいる系の時間をtとし、τはtとその空間座標であるx,y,zを使って、τ(x,y,z,t)で表せるとします。そこで、上の式を『書き直して』、

とアインシュタインはしています。著者はここにも反論します。ただ単にτ₀，τ₁，τ₂を、一般的な関数としたτ(x,y,z,t)に書き直しただけの式に対し、

逃げる泥棒とすれ違うより追いかける方が時間がかかるように、運動している線分上を光が往復すれば復路よりも往路に時間がかかり、運動系の記述とは一致しなくなります。

と述べます。つまり、装置が動いていると見る系では、光源から反射板へ到達する時間の方が、反射板が速度vで逃げているので長くなり、反射した後は、逆に光源が近付いてくるから時間が短くなると説いています。もちろんその通りです。

もし書き直した式が、装置を動いていると見る座標系として、

1/2（ｔ₀+ｔ₂）=t₁

となっていたら確かに間違いですが、このような式はどこにも出ていません。すなわち、著者の反論すべき式は、巻末のアインシュタインの6月論文の中には全く出てこないのです。著者はここで詰ってしまって、相対論の論文の先を見ていないようですが、これは単なる著者の勘違いだと思われます。

なお、復路は時間が短く、往路では時間がかかるという事実は、上述した式の

x'/(c-v) + x'/(c+v)

の部分がまさしくそれです。

著者が反論している 1/2（ｔ₀+ｔ₂）=t₁ はアインシュタインの論文にないという指摘です。まるで著者が捏造した式で誤りを指摘しているかのような書き方ですが、この式も木下氏が勝手に追加した式です。

誤った式があるはずなのにどこにも見当たらないなら、自分の判断が間違っていると疑ったほうがいいかと思います。さらに調べても見つからなくとも、このような非科学的な方法で批判をするべきではありません。ありのままのデータを使わなければ, 科学も成立しなくなってしいます。

ここでの議論では、論考の(7)式と(8)式が対象になります。

１と２は密接に関係しています。

(7)式のτ₀、τ₁、τ₂は時刻を表し、括弧はそれをまとめる役割を果たしまます。一方、(8)式のτは共通の未知関数を意味し、括弧に内に各関数のパラメータが入ります。本文でも説明していますが、τの意味が変化すると同時に、括弧の意味も変化していることを抜きにしてこの議論は成立しません。

(8)式の先頭にある「１/２」は関数の括弧にも入ってないので、関数のパラメータではありません。つまり、この値は相対論で求める関数τの影響を受けず、式の左辺と右辺のバランスを保っています。

そして、左辺は原点の時刻と往復にかかった時刻、右辺は原点の時刻と往復後の時刻です。（アインシュタインの論文は時刻と時間も不明確ですが・・）

結局、式にすると1/2（往復の時間）=（往路の時間）となり、木下氏がどこにもないと述べている 1/2（ｔ₀+ｔ₂）=t₁と同じ構造になります。

要するに、式の構成について指摘していることを理解できなかったので、そんな式はどこにもないと決め付けてしまったようです。

次に、著者は、観測者が速度0、速度1、速度vで動く場合、極端には光に乗って光を見た場合に、その光速度は、

光速度不変ではすべてcと答える事ができます。あなたは？　やはり運動している観測者の速度に関係なく光速度はcですか？　それぞれのデータ、0や1、vやcはどうなったのでしょうか。それらをすべて無視しませんでしたか？

とします。声を大にして言いましょう。無視はしていません。運動する観測者の速度を取り入れて、なおかつ光速度はcなのです。

この部分は、相対論を信じている人の中にも多くの誤解を生んでいますので仕方がないかもしれませんが、光速度が観測者の動きは無視して常にcなのではなく、観測者の動きを考慮してもcなのです。

・・・略・・・

決して計算していないのではありません。

本文の「最終解答へむけて」で指摘しているように、

相対論に反対する人だけでなく、相対論をブルーバックス程度でカジッた人でも光だけ特別としてしまう風潮があるために、このような間違った指摘がまかり通る事になります。もちろん経緯としては光速度不変が先にあって、それに合うように速度合成則が算出されたのですが、決して光だけが特別だとして扱っているわけではありません。

著者の主張している速度合成則は多分、

V=V₁+V₂（ただし、0≦v＜c）

c=c（cには何足してもc）

というような、cだけを特別扱いしたものでしょう。相対論はそんな理論ではありません。

本当に相対論を理解して批判しているのかさえ怪しくなってきました。

・・・作成未定・・・

［マイケルソン・モーレーの実験について］

この本の中で、もっとも下らないと思われるミスはここにあります。

著者はマイケルソン・モーレーの実験の類似思考実験として、45度の傾きを持った鏡にぶつかる光を考えています。そして、鏡が止まっていれば（図のような場合）光は90度反射されて真上に届くとしています。ここまではよろしい。

ところが、鏡がvの速度で光に近付いたりすれば、光は真上では無くてナナメ前方に飛ばされるとします。つまり、著者は光をサッカーボールと同じようなものとして扱っていて、反射すると鏡の速度がベクトルとして加わると思っているようです。 マイケルソン・モーレーの実験は、エーテル内を飛んでいく光の波を考えていますが、波はそれを伝える媒質に対して常に同じ速度で動きます。反射鏡が動こうが光源が動こうが関係ありません。

このような、反射鏡による光の速度変化の主張を堂々と述べているのは、本書の中でも日高氏だけです。窪田氏もその他誰もが、少なくとも波としての光の性質だけは間違えていません（他の著者が指摘しているのは、エーテルに対して動いている観測者が見る光速度についてです）。この波の性質は中学校で習ったと思いますが…いや習わなくても水面の波紋を見れば誰でも理解出来る筈です…。

また、続いてこの著者の勘違いをさらに決定づける端的な思考実験もあります。マイケルソン・モーレーの実験で、エーテル流と平行に走る光の方の考察で、行きの光の見掛けの速度がc-vで、帰りがc+vとする部分に、著者は反論します。この部分に反論する人も、本書の中では日高氏だけだと思います。

図のように時速100kmで走る列車があり、101kmで飛ぶボール（ここで既に波ではなく、物体を登場させている）があるとすると、列車内部では、101-100=1であり、時速1kmの速度のボールに見える。マイケルソン・モーレーの実験では、行きはc-vだからいいとして、帰りはc+vだから、この考えをボールに当てはめると、この計算は、

列車内で時速1kmで壁にぶつかったボールが反射すると時速201kmで跳ね返ると述べている！

と同じだと主張し、マイケルソン・モーレーの計算を間違いだとするのです。ここまでくるとさすがに目がテン(･_･;)になってしまいます。

船が時速100kmで航行していて、後ろから波が時速101kmでくれば、船上では、時速1kmで近付いてくるように見えますし、一旦反射して船と逆向きに走り出した波は、時速201kmで離れて行きます。波なんだからそれでいいんです。

…ところで、この本には監修っているのでしょうか？

監修は、竹内薫氏です。本人はとぼけていますが・・・。

・・・作成未定・・・