２つの封筒のパラドクスの結論だヨ

ネットを見ても「２つの封筒のパラドクス」の本当の原因はハッキリしない。正解とされている解説の多くが、「確率」と「期待値」を計算することに夢中になっているような感じ。じゃあ、このあたりをもう少し検証してみよう。

---

期待値計算の「＋」が迷宮への片道切符

意外と多いのが、「交換した方が得」という解答。

なーんて解答は、説明するまでもなく論外。どうやら、大学の先生なんかがもっともらしく解説したり、本に書いてるから正解だと勘違いされてるようだネ。早く訂正してたほうがいいと思うヨ。

一般的にもう少し慎重な解答例はというと、

これは、うーんいい線いってるかなって言いたいけど、この先が続かない。なぜ続かないかと言うと、これもいきなり「２つの封筒問題」から脱線してるから。

上の２つの解答例で共通して問題になるのが「＋」というプラス記号。先に説明したように、この「＋」は、もともと同一のイベントの確率を１に戻すために使うもの。そして、異なるイベントの確率を足し合わせるために使ってしまうと、新しいイベントを生成してしまう副作用がある。

手持ちの金額がＡ円だと認識したあたりから、Ａ円の封筒を中心に残りの封筒をひと固まりと考え始めて、頭の中にあった０.５Ａ円、２Ａ円、が同じイベントに共存していると錯覚して、

というアンイな考えで、それぞれの出現確率を「＋」でガッチャンコしちゃった。

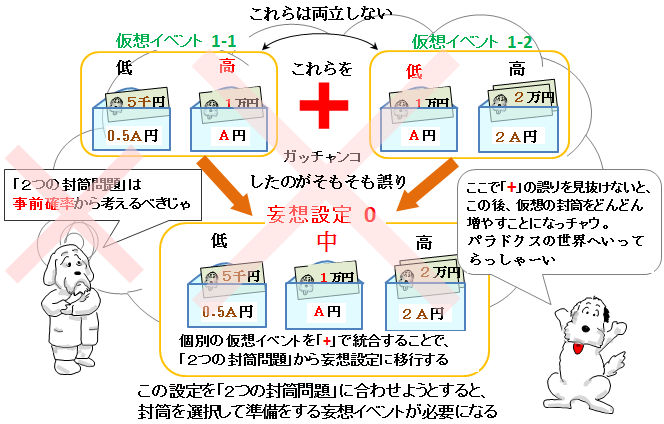
この統合によって、独立した２つの仮想イベントにあった、０.５Ａ円、２Ａ円、そして共通金額のＡ円が、同じイベントに存在する封筒の金額として再設定されたことになる。このように「２つの封筒問題」ではありえない３つの封筒を設定してしまう「＋」の使用の是非について、ほとんど議論されていない現状では、

使い方を間違わなければ、「２つの封筒問題」の解答に「＋」なんか必要ない。つまり、期待値計算の式に「＋」が入っている解答はほとんどが誤りだってことになる。

この先もまだまだ説明しなきゃならないことが山ほどあるってことは、やっぱり未解決問題だよネ。

---

事前準備ありなしの比率が未知のまま

手持ちの封筒に対して予想した２通りの組合せを「＋」で統合したために３種類に増えてしまった。もちろん、このままでは「２つの封筒問題」の出題に使えないので、３種類の封筒から、封筒２つを選択する事前準備のイベントを想定しなきゃって流れになる。

ということで、どうやって２種類の金額の組合せを選んだか、出題者のフトコロ具合から心理学の話まで出てくる。おまけに金額の上限や奇数だった場合とか、本題とは関係ない話で手がつけられなくなっていく。

そもそも、

３つの封筒が関わっている事前準備のイベントのことを考える意味もなくなるから、期待値を計算している式もいらないってことだネ。

それはそうだけど、もともとは、封筒３種類を同時に妄想したから必要になった式だよネ。封筒が２種類しかないなら、αに０か１を代入して計算するまでもなく、式の存在理由がなくなるネ。

つまり、

もともとは、「２つの封筒問題」の参考にするために、起こりうる可能性をありったけ出しつくして期待値を計算したかったはず。ところが、「２つの封筒のパラドクス」で、封筒が３種類ある「事前準備あり」の可能性について考え始めると、この限定された条件に合ったパターン内だけで結論を出してる。

事前準備の「事前準備あり」パターンについて考えたなら、「事前準備なし」パターンについても考察しなければ、「２つの封筒問題」の準備のパターン全体で確率１にならない。

封筒が２つしかない「事前準備なし」の確率をβとして、そのカラクリを図示すると・・・

　　　

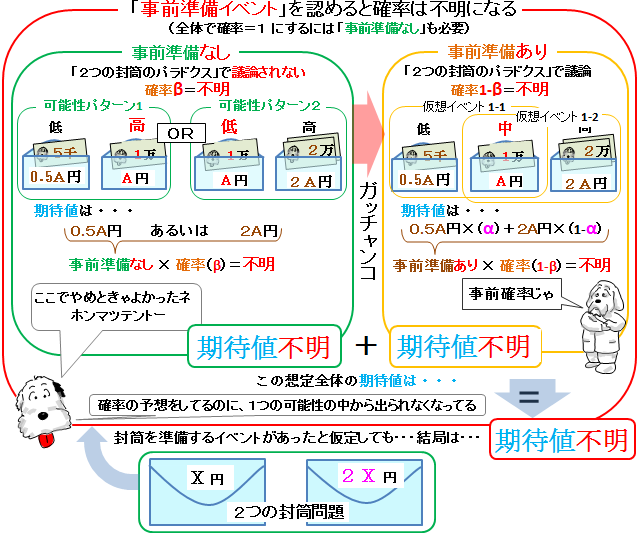
封筒が２種類しかないと仮定したなら、準備イベントも不要なので３種類の可能性は消してしまって何も問題ない。逆に、封筒が３種類以上あると仮定してしまった場合は、余計な準備イベントの可能性が追加されただけで、「事前準備なし」の可能性を消していいわけじゃない。

期待値の計算式まで見せている解答例は、「事前準備あり」の想定の中だけで結論を出して、「２つの封筒問題」の結果だと思い込んでる例がほとんど。「事前準備なし」のパターンについて何も考えないまま終わっている。

問題の封筒が２種類そろうまでの考察として、「事前準備あり」と「事前準備なし」の合わせて２パターンの可能性がある。２つを合わせた全体で確率１になるから、「事前準備なし」の確率βが不明なら、「事前準備あり」の期待値をどれだけ必死に計算したところで、全体の期待値は依然として不明のままだヨ。

封筒が３種類以上あると勝手に想定して「２つの封筒問題」を解決しようとすると、知らないうちに次から次へと未解決問題がたまっていくシクミ。スゴイ問題だネ。

---

不要な数値があり、必要条件も表現できない式が正解？

事前準備まで考えると、封筒の種類はどうしても多めになるのは想像できるけど、本題で使う封筒は、はじめから２つだけ用意してあったってことでいいんじゃない？

式が存在しえないという考察だけでは、まだ使おうって人がいそうだネ。あらゆるパターンの可能性を考えなければ正確な確率を求めることができないのもよくわかるし、見落としがあったんじゃ正しい答にたどりつけないのもわかるヨ。

数学的に厳密な答を出そうと、ほとんどの人が可能性のある封筒や数値の、あんなことやこんなことを想像して、もうこれ以上慎重に考えなくても大丈夫と思うくらい可能性を出しつくしているみたい。

でも、「事前準備なし」の確率を認めた場合、絶対に見過ごせない別の「確率」が顔を出してくる。それは、仮想のビデオ撮影で確率１の組合せを判断するでも触れたように、

ということ。

について、０.５Ａ円か２Ａ円のどちらか一方は、必ず無関係な金額になる。いろいろと不明な設定が多い「２つの封筒問題」で、確率１で必ず発生する事象として、

何も知らない第３者が式を見て何を期待するかという観点から考えてみると、前者は、同じ封筒で問題を何万年繰り返しても出てこない金額を期待させるし、後者は、答がはっきりしていないので解答しているとは思わないかもしれない。

出現しないものを期待させるより、はじめから「どっちかわからない」と言ってあげた方が親切な気もする。正解を知っている出題者が、見たこともない金額が入った「不可解な計算式」を見せられるのと、「０.５Ａ円か２Ａ円のどちらか」と解答されるのではどっちがガテンがいくだろうネ。

やっぱり数学の問題だからネ。余計なものがない方がいいに決まってる。

じゃあ、その式のαに数値を代入して、「０.５Ａ円の場合」と「２Ａ円の場合」が計算できてから、「事前準備なし」の解答に使うプロセスを見てみよう。

　　

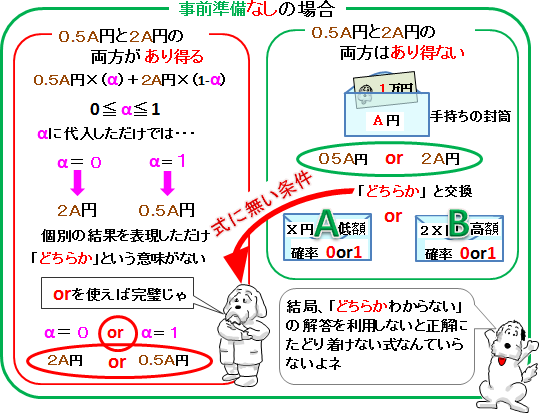
ここで着目するのは式を成立させるための条件の出どころだヨ。この構図で根本的におかしなことに気付かないかなァ。

「or」は、「２つの封筒問題」で「わからない」と答えるときに出てくる。どっちかハッキリしないと考えたときの解答で中心的な役割を果たしている。

期待値計算に使う式には、はじめからそんなものはない。計算し終わっても、「０.５Ａ円の場合」が出て終わり。あるいは「２Ａ円の場合」が出て終わり。個別のパターンは個別に数値を代入して計算したらそれで終わり。「どちらか」という二択の表現はどこにもない。

「わからない」という答が、二択のデジタル的構造だとすると、期待値を計算する解答は比率が変動するアナログ的構造。αに代入する数値を変えれば、１つのパターンは計算できるけど、どちらか不明という場合の複数パターンについては表現しきれない。

これを無理やり「or」を借りてきて、「０.５Ａ円の場合」or「２Ａ円の場合」という構成に変えようとすると、それはそれでまた別の問題が出てくる。

２つの式の寄せ集めた構造を認めてしまうと、

あらゆるパターンを表現できているはずの式は、実は計算値にしか着目していない。構造まで解析してみて初めて「２つの封筒問題」の論理的条件に対応できていないことがわかる。おそらく、専門家が悩まされているパラドクスの一部は、この矛盾する構造に起因している。

足りなくなって急に借りてきたり、条件違いの式を複数用意しなければ正解を表現できないなら、単純な「どちらかわからない」の方が数値的論理的に、より正解にふさわしいと思うナ。

もっとも、「２つの封筒のパラドクス」で、なにか困ったことがあると必ず「２つの封筒問題」の考え方の助けを借りながら問題を継続する構造は、気付かないふりをしてればもう少しパラドクスで楽しめそう。

---

可能性のあるパターンは未検証で未知だらけ

金額を仮想して、みんながやっている余計なことで説明したように、２つの仮想イベントを想像した段階で、低額か高額のどちらかしかあり得なかったＡ円を２つのイベントを足し合わせることで、解答者は手持ちの金額Ａ円を中心に期待値の考察を始めてしまう。

３つの封筒が準備されていたと考えてしまうと、またまたややこしい問題が出てくる。

そういった考えも２つの封筒しかない場合で考えた結果を組合せているからこそ成立している。準備イベントで用意された３つの封筒のうち、中間の金額が必ず手持ち金額Ａ円になるなんて、そんな奇妙なことある？　

そうなのダ。「手持ちの金額を見たところＡ円であった」というのは、あらゆる可能性を考えたパターン全体ではなく、特定のパターンだけを抜き出した結果にすぎないのダ。

つまり、３つの封筒に設定変更されたにもかかわらず、

どう言うこと？　

「２つの封筒問題」で手持ちの金額を見て想像したのは、あくまで低額、高額しかない場合の選択肢であって、３つの封筒を想定してあったわけじゃない。「２つの封筒のパラドクス」のように、はじめに封筒が３つ準備されていた想定に設定変更するなら、手持ちのＡ円は中額だけでなく、低額、中額、高額の可能性が出てくる。

　　

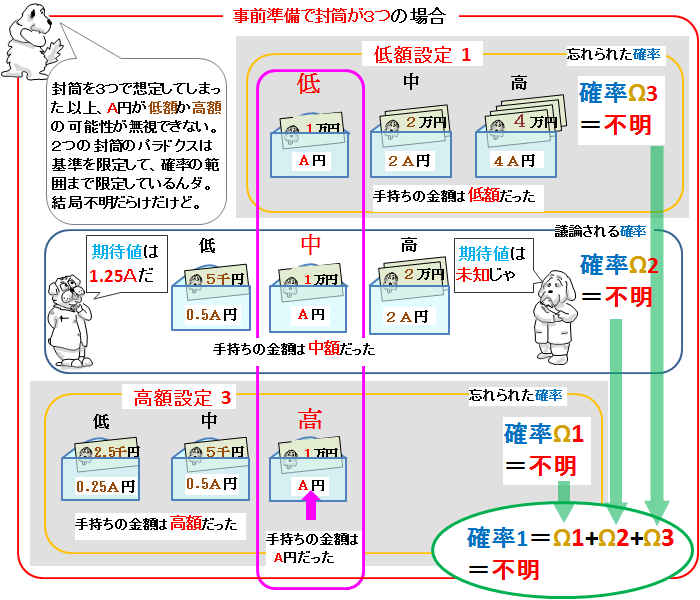
これらの確率を全部足して、やっと手持ちの封筒にＡ円が入っていたすべてのパターンから形成される確率１が成立する。それぞれのパターンの確率を求めないと交換した時の期待値の話ができる状態にもならない。中額だけに限定した期待値計算の議論は、Ａ円が低額や高額だった場合の期待値計算のことを全く忘れてる。

「２つの封筒のパラドクス」の構造は、議論の的になっているテーマの外側に、さらに未知の確率が入れ子のような構造で覆い尽くしている。どんなに慎重に個別の確率を計算しても、そのさらに外側にあるイベントの確率が不明じゃ期待値の出る幕もないネ。

ここまでの情報で「２つの封筒問題」から「２つの封筒のパラドクス」に移ってからの仕組みや疑問を説明できそうなので、全体の構造を確かめながらまとめたヨ。

「２つの封筒問題」には基準がない

　　

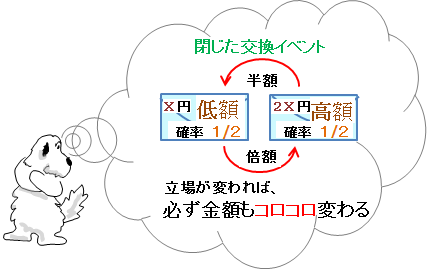
「２つの封筒問題」は、単純に２つの封筒を交換するだけの閉じた交換イベントになっている。まずこれを意識できているかどうかで解答の方向性がまったく違ってくる。

　　

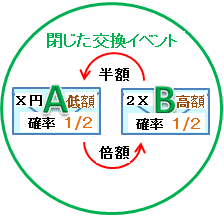
この閉じた交換イベント全体を眺めるようにして意識できている人は、「封筒は２つしかない」し、確率は「１/２」のまま変化しないという性質から、何度交換を繰り返しても手持ちの金額は低額と高額を行ったり来たりするだけとわかる。

そして、この２つの立場をまったく同等に扱って、この後、封筒の組合せや自分の持っている金額の情報が入って来ても、相対関係を解明する基準に関する情報でなければ、「わからない」と解答できるはず。

つまり、「２つの封筒問題」は、

ということに気づき、これ以降の余計な情報に惑わされないことが重要になるんダ。

---

勝手に基準を設定！

さて、基準が存在していないために答が出せないとわかっていても、確率や期待値計算で損得を計算できる手法を知っていると、

または、

というように、計算に使う基準を相対関係を決定する基準（立場）と同じものだと勘違いしてしまう。

そんなときに、タイミングよく

という情報が入ると、早速、計算をはじめる。

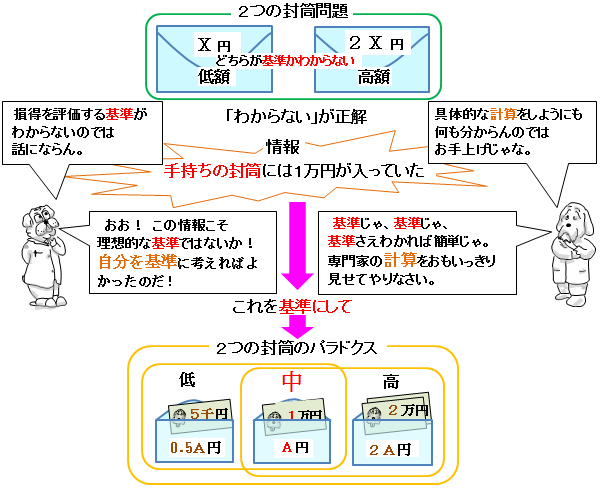
自分を中心に様々な可能性を考えて、具体的な数値がどんどん計算できるから、「手持ちの封筒には１万円が入っていた」という情報こそが、「２つの封筒問題」の突破口になったと勘違い。

でも、閉じた交換イベントを意識できていれば、

ことに気がついて、これ以上準備イベントの議論が無意味だとわかるよネ。

その結果、仮想的な期待値計算を「＋」で統合してしまうことで、封筒が３つ以上になり、組合せの可能性が増える。さらに設定が書き変えられて、さらにその影響で設定が書き換えれて・・・と、どんどん拡大していくという仕組み。

事前準備のイベントに気を取られてると、今度は事前準備なしの考察がおろそかになる。

様々な可能性を追求していくと同時に、裏では未検証の可能性もどんどん増えることになる。

結局、「２つの封筒のパラドクス」は、誤った基準を仮想して結論を出そうとしたものの、確率や期待値の問題がいつまでも解決しないので、

ような巧妙な仕組みになっている。

---

パラドクスの原因は汎用式というデタラメ

根本的な原因に迫るために、問題の設定をおもいっきりシンプルな表現に変えてみて、「交換するか」を決定するために本当に必要な要素を絞り込んでみる。

というように、相対関係を評価する立場がわかる情報さえあれば、数値計算をするまでもなく結論が出せる。

そして、解答者の意思に関係なく、得をするなら必ず交換という条件でなら、「交換するか」という問いは、選択している封筒について問われていることになる。

この場合、「１万円が入っていた」という情報が与えられても、「わからない」という結論を出せるのは、計算方法が確定していない単独値「１万円」によって、パラドクスが必然的に起こるわけではないことを示している。

先に説明したように、「２つの封筒問題」は、閉じた交換イベント内の相対関係を問われているにもかかわらず、それを判断するための基準を確定していないという構造上の欠陥があったよネ。

だから、ここでどんなに慎重に式をたてたとしても、結局、式は使えないまま、用意された数値も処理されないことになる。

そう、

本来なら、低額か高額それぞれの立場で使う２つの式を作って、相対関係の評価をしたいところ。そのわからない部分を確率で表現するというアイデアが広く受け入れられた引き換えに、簡単な条件が見過ごされることになってしまった。

そもそも評価の基準（個別の情報）をあいまいにした汎用式で、個々の相対関係を評価しようというのが無理なハナシ。両方の立場に適用して、

なんて主張に出てくる汎用式は、低額か高額の立場が判明している状況では跡形もなくなってしまう。適用先が不明のときだけ現れる式から判断するなんて、予想じゃなくてデタラメと呼んだ方がよさそうだネ。

---

結論、実体は複数の「２つの封筒問題」

「２つの封筒問題」が「２つの封筒のパラドクス」になってしまう要因はいろいろあったけど、

という最終的に得するようなルールで交換するなら、閉じた交換イベント内で自分の持っている金額がコロコロ変わるだけ。確率は１/２のまま変化しないので正解も分からないハズ。

なのにどうして、値を見ただけで、無駄なシミュレーションしてみたり、難解な理論を引っ張り出して答を見つけようとしてしまうんだろ？

確かに、あらゆる可能性を無視できないような気もするけど、間違った解答を主張しているのは数学が得意そうな人たちばかり。期待値を使った数学的解決を宣言する前に、結構アンイに使ってる確率についてもう少し考察した方がいいんじゃない？

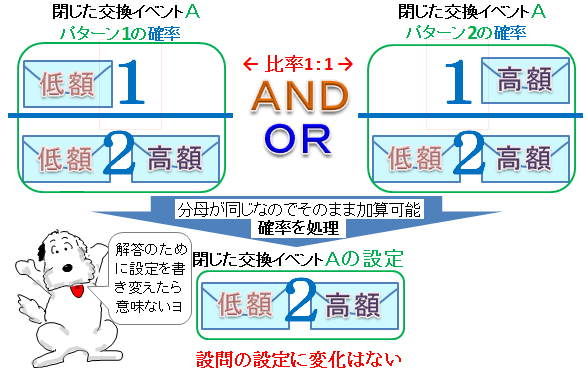
一般的に問題解決の糸口を探そうと、あえて設定や方法を変えてみることがあるよネ。解決の確率を高めるために、新しく考えたあらゆる方法を「and」で加算するうちに、最初の設定とは違ってくる。このときの確率は設定を変える前提で使われる。

今度は、数学でよく使う確率について考えてみる。もちろん例外はあるだろうけど、先に設定が決められていて、後から確率を問われる問題なら、決められた設定や方法の範囲全体を１として起こりうるパターンを確率計算することになる。

もし、見つけたパターンが決められた設定や方法の範囲１に収まりきれない場合（「２つの封筒問題」では、封筒は２つしかないという設定）、確率計算式を「or」で複数の解答に場合分けしたりして、設定が書き換わるのを回避しなければならなくなる。

このような確率の違いを意識していれば、「and」で加算する確率を数学的解決に採用してしまったとき、問題設定の変化から間違いに気づくハズ。

ところが、「２つの封筒問題」で金額が低額か高額の組合せしか考えられない基本段階では、同じ設定に対する２つの確率なので分母を通分する必要がない。そのために、確率計算によって問題の設定が書き換わることもない。

これは、数学的に「or」の確率を使うべきところで「and」の確率を使ったとしても、

ということ。

そして、この先で金額を仮想した時にようやく間違いの効果が表面化してくる。

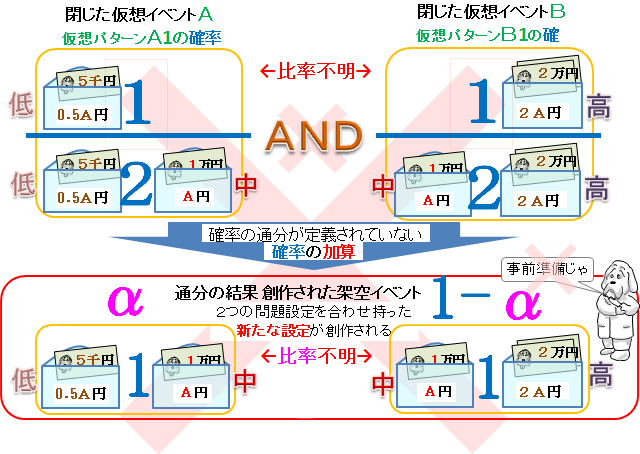
「and」を使う確率で通分したために、想像したあらゆる設定が「and」されて、３つ以上の封筒から２つを選択する事前準備や、その事前準備の確率を求める問題の設定のように勘違いされて脱線が始まる。

複数の異なるイベントを処理したものは、事前準備でもなければ確率を求めるサンプルでもない。「２つの封筒問題」から飛び出した架空の設定だから、シミュレートを繰り返しても数学的意味はないよネ。

また、３つ以上の金額が同時に存在出来ないと気づいて出現率のαに0か1を入れたとしても、「or」の確率を使ったのと同じ効果で、パラドクスを回避できる。

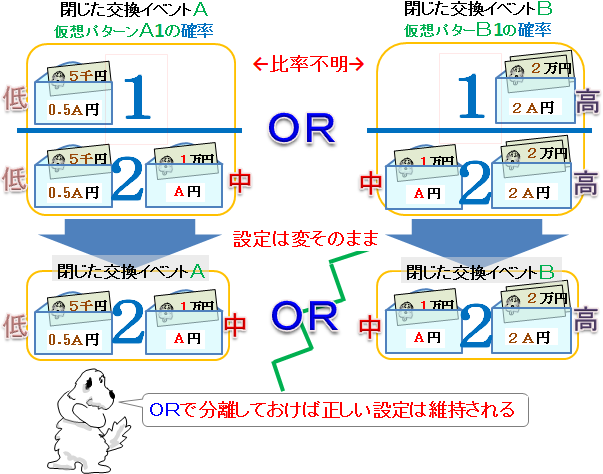
ようは、設問の基本設定を書き換えなければいいんだけど、金額を仮想する手順そのものに間違いがあるとは思えないよネ。それなら、もっと根本的な指摘をしておこう。
　●　一旦、用意（設定）された封筒の金額は変動しない
　●　解答者が金額を予想した時点で交換の是非が決定してしまう
以上のことから、・・・

手持ちの封筒に１万円が入っていたら、

「２つの封筒問題Ａ」と別の組合せなら、別の「２つの封筒問題Ｂ」として、

「２つの封筒問題」の出題が１回だけなら、実際に用意されるのはどちか１組だけ。金額の予想をした時点で、アタリかハズレどちらかになる。別パターンを含めた確率まで考えてしまうと、違う設定の問題を追加したことになるんだ。

もちろん、交換の是非は「ワカラナイ」が正解というのは変わらないヨ。

つまり、２つしかない封筒の問題を複数寄せ集めて、確率論を展開した結果、「２つの封筒のパラドクス」になって、同時に存在出来ない金額の期待値から「交換した方が得」と判断していたなんて、数学以前のバカバカしいオチだネ。

「ワカラナイ」ことがイッパイあるから数学はおもしろいんだヨ。

相対性理論とそっくり

２つしかない封筒の問題をわざわざ複数集めて別の問題を作って悩んでいた「２つの封筒問題」だけど、解決の糸口を探っているつもりが、大量の誤答で頭の中が埋め尽くされるような構造を持っている。重要なのは問題を解いちゃダメだってこと。

もし、「２つの封筒問題」で、回答者自身が問題を書き換える特徴を捉えることができたなら、同じような仕組みで誤答を量産している相対性理論の本質を見破れる可能性があるヨ。

誰が計測しても光速が一定になるように、観測者ごとに時間と空間のスケールを変える理論を提唱したアインシュタインは、

これのどこが誤りなのか・・・。

って話。

せめて暗算の存在を記録しとかないと、数字が合わなくなった原因がかわからなくなるからネ。そう、アインシュタインはこれを忘れたから、時空をゆがめて「解決」してしまったワケ。

「２つの封筒問題」とは比べ物にならないほど深刻な問題を引き起こしている相対性理論のナゾも、「解決」を急がずに、ていねいに解析するとナゾが解けるはず。理論が完全に崩れる前に挑戦したほうがおもしろいヨ。

まずは、アインシュタインが相対性理論を発表した論文をまず読んでみよう！
「運動している物体の電気力学について」について