 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 天の声 | トリック紹介 | 相対性理論とは | 疑似科学書解説 | 検証実験などの再検証 | 雑 記 帳 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 2004/03/14 |
|
 1994/01/31 相対論を打ち砕く シルバーハンマー |
||||
|
2005/01/02 開設 |
||||||
アインシュタインの「相対性理論」や理論物理学は、
変換関数の見落として発生するローレンツ係数による「数学トリック」です。
数学の基礎が理解できていない人ほど「相対性理論」の正しさを主張して誤った情報を拡散する傾向があります。ネットや書籍の情報を鵜呑みにする前に自分の力で「数学トリック」を見つけられるようにしよう!
 0.天の声
0.天の声
物理学の素人が現代物理学の基礎理論に異を唱えるきっかけ。
 1.天の声
1.天の声
 2.あきれた現代物理学 (準備中)
2.あきれた現代物理学 (準備中)
 3.科学とは (準備中)
3.科学とは (準備中)
- マイケルソン・モレーの実験式は反射の法則が見落とされている
- 電磁気学は演算子「外積」の座標変換が見落とされている
- 電磁気学でcが一定の証明は、基準にしたcを再摘出しただけ
- ローレンツ変換係数は誤った数学の手法で発生する誤謬
- アインシュタインの特殊相対論の論文は、先人の誤りを盗用した辻褄合わせ
- 相対性理論は前提、考察、処理方法において100%誤り
- 光速度不変の原理は太陽と月の観測だけで反証可能
- E=mc2は無意味な架空の式
- 等価原理は次元を減らして同一視するだけの単純な論理トリック
- 相対論的効果を主張する際のGPSと同じ原理で運用されているGPSは実在しない
- 一致しているはずのアインシュタインの日食の予想計算に根本的な誤りがある
- 物理学の記述方法としてガリレイ変換を選択するのは必然
- 古典力学を修正するなら、加速度の定義から見直す必要あり
- 宇宙エレベーターは原理の式から誤っている
- フェルマーの最終定理を解決したワイルズの証明に誤りがある
- ポアンカレ予想の解決に物理学は使えない
- リーマン予想は数学の本質ではなく、記述法の不備からきている
- 角の3等分不可能の証明には誤りがある
- 潮汐は地球の自転が影響している
- 月は自転していない
- 2つの封筒のパラドクスの解説は、ほとんど誤り
(反論やリクエストがありましたらご連絡ください。)
 相対論の光速度cは定数じゃなくて、
相対論の光速度cは定数じゃなくて、みんなが暗算で一定にしている「速度不変の原理」の解だヨ。
はじめからcを関数扱いして式を解けば、暗算と同じ「C+v」が導出されておしまい。
光やニュートリノの速度なんて全然関係ないし、cが関数だってうわさが広まった時点で、
カミオカンデ・スーパーカミオカンデ・ハイパ―カミオカンデ
KAGURA・相対論的ナンチャラ・・・
相対性理論も宇宙論も重力波もみーんなおしまい。チャンチャンッ。
すでに数千憶円の税金が
数学のルールを無視した相対性理論の検証に浪費されている
自然災害の多い国だからこそ、科学研究費は、
災害対策や人命救助などまともな研究に使ってもらおう!
相対性理論で税金が浪費されなければ、
1千万円規模の研究が1万件できる。
どんな研究成果でも、検証に応じない妄想理論より役に立つ。
そのために必要なのは・・・
一人でも多くの一般人が、紙と鉛筆でできる相対論の検証に参加すること
物理学を覆す発見は日本から発信しよう
理論物理学の脱線は、座標変換とガリレイ変換に対する認識不足から
物理現象を直交座標と絶対時間で表現しているニュ−トン力学では、ガリレイ変換が純粋に数学上のデカルト座標系の変換と一致する。この事実は、ニュ−トン力学で物理現象を取り扱うより先にガリレイ変換は「記述法」の一部として内在していることを示している。
物理現象を記述するためにはさらに理論と方程式を追加しなければならないことからも、古典力学の不備を解決したいのであれば「記述法」であるガリレイ変換を崩すことなく理論や方程式の修正に着目する必要がある。
相対性理論に代表される理論物理学は、ガリレイ変換をニュ−トン力学の方程式と解釈して、ガリレイ変換ニュ−トン力学従わない時空理論を物理学に据えているが、当然、「記述法」の変更による効果以上の成果を見いだすことはない。理論物理学者自ら「記述法」を崩壊していることを認識し反省しない限り、物理学の発展を阻害する理論暴走を止めることはできない。
相対論由来、潮汐力の「遠心力」を「慣性力」書換え、教育への悪影響が加速中
相対性理論の誤った座標変換が蔓延すると、複雑な物理現象も簡単な動きに変換しさえすればスッキリ説明できると錯覚する学者も現れる。この誤った手法を使って、昔から諸説ある潮汐力の説明に使われてきた「遠心力」を「慣性力」に改めさせようと活動している人達が目立ってきた。
この主張は、地球の自転を無視し、地球に存在しない仮想質点を設定したかと思うと、遠心力に比例する簡単な図形の線分だけをベクトル分解して「一様な慣性力」が地球全体に働いているとしている。この主張は、月の公転を逆回転させる奇妙な座標系に移動して考察した結果だ。現実の質量を考慮しないで力に言及してしまうのも、仮想実験を過信しすぎた理論物理学の影響と言える。
地球のどこでも同じ「一様な慣性力」は、簡略的な図形の数点にだけ置かれて潮汐力の説明は終わってしまう。球体である地球の全質点に働くなら説明とは異なる合力になってしまうという不都合な力学的考察は一切触れない構成になっている。
この活動に影響されて、国立天文台や気象庁は詳細な説明を避けるかたちで「慣性力」と書換えてしまった。「遠心力」も「慣性力」の一種だから間違いではないが、議論を重ねる科学の様相はない。ネットで調べればいくつも見つかるので信じる前に自分達で検証し議論した方がいい。学生が直接目にする教科書もターゲットになっているようなので、蔓延しないよう今後も注意が必要だ。
疑似科学者の学識レベルが分かる 松田卓也氏著「間違いだらけの物理学」書解説
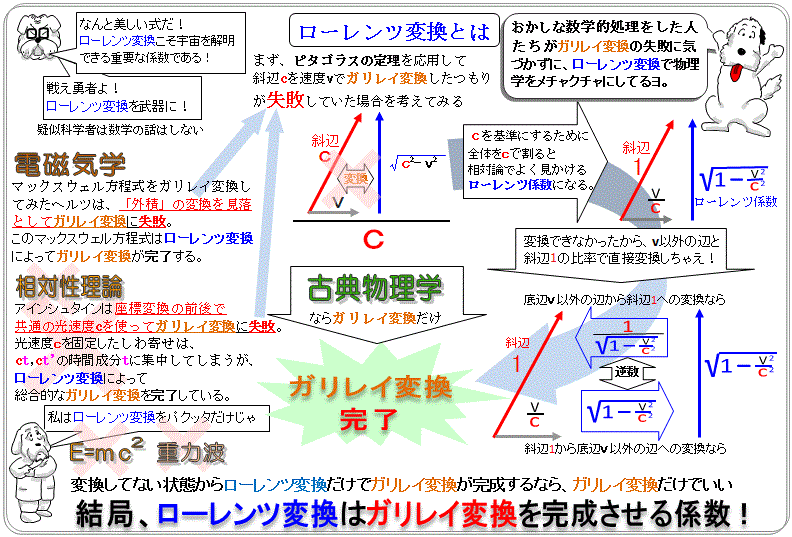
数学と座標変換の無知がローレンツ変換を発生させる
数学、特に座標理論の知識の乏しい学者がニュ−トン力学に不満をいだくと、基本的な数学や座標理論の基礎が身につかないうちに時空を扱った辻褄合わせの理論構築を急ごうとする。それらの理論に共通して発生するローレンツ変換係数について、新たな導出法が学術的高評価を受けるほど特別な扱いを受けている。ただ、このような係数は自然界には存在していない。
「記述法」として変更を加えられないガリレイ変換を理論物理学者自らが独自の誤った演算処理によって無理やり修正したことで、それを補うためにローレンツ係数は発生する。物理学も数学でもない、単なる誤謬からのローレンツ係数の導出法が学会で取り上げられることもないのでここで簡単に説明しておくことにする。
原点や座標値の存在しない座標変換理論
MM実験を含む多くの実測実験では速度と距離といった座標系の差異を主なデータとして扱うため、座標理論では欠かすことの出来ない原点や座標値は重要視されない傾向がある。同じ内容を座標理論で標記すれば必ず基準となる座標系の存在が浮かび上がるが、座標理論の知識が不足している場合、座標系に速度や距離データを直接取り込んで、シンプルなガリレイ変換式からローレンツ変換式を創り上げてしまう。
簡単なガリレイ変換の例として、時速100kmで走行している車から時速300kmで並走する新幹線の速度について考える。新幹線の速度をC、車の速度をvとして、記述系である車から見た新幹線の速度は、
(記述系から見た観測対象の速度)=(観測対象の速度)−(記述系の速度)
(時速200km) = (時速300km) − (時速100km)
となる。変換式は、
(記述系から見た観測対象の速度)= C − v
となり、ガリレイ変換が成立していることがわかる。
次に逆方向に進む新幹線の速度についても考えてみる。
(時速400km) = (時速300km) + (時速100km)
観測対象と並走していた時に減算されるvが、向かってくる時には加算される。かといってガリレイ変換が
(記述系から見た観測対象の速度)= C + v
に変化したわけでないことは誰でもわかる。ベクトルを座標値で表現する座標理論で表現すると、逆向きの速度の符号が負になり、ガリレイ変換は不変に保たれているのが確認できる。
(時速+200km) =(時速+300km) − (時速−100km)
このように座標理論では座標値を丁寧に扱わないと、不変の方程式を変化させたような記述にしてしまうことがある。アインシュタインは、先人の誤ったガリレイ変換式(C-v)と(C+v)をそのまま座標理論に取り入れたために歪んだ物理法則にさらに修正と調整を加える。ただしアインシュタインのローレンツ変換導出法は誤りから偶然に導出できたのではなく、先にローレンツ係数があり、(C-v)と(C+v)から導出するよう無理やり調整したと考えるのが妥当だろう。
ちなみに、MM実験の検証式でマイケルソン氏は反射の法則の見落としから光の往復を(C-v)と(C+v)としている。ここだけを眺めるとガリレイ変換式を変更しているようにみえるが、座標理論の誤りとは性質が違うのでここで詳細は説明しない。
MM実験式の誤り指摘と修正例 実験式を修正しよう!
各座標系の方程式を同等にするという不要な要請と係数と関数の混同
古典力学の方程式が変化すると勘違いし、電磁気学やMM実験の解釈やどの座標系でも変化しない光速度の情報から(C-v)と(C+v)をすべての座標系で同等にしなければならないと判断すると、今度は数学の関数を使った方法へ移る。誤りを再現するために古典力学の光速度Cと光速度不変の原理に従う光速度cは同じ表記とする。
往復で同等の法則が介在して光速度を不変にしていると考え、まずはそれぞれを変換関数Sで表記する。 S(c-v)=c、S(c+v)=c
Sは括弧の中を同一にする速度の変換を表している。本来、関数は必ずしも式である必要はないため、このような関数式は無限にある解の特定ができない。ここまでの誤謬を理解している場合は、左式はそのまま、右式の括弧の中の「+」を「-」に変換する関数と考えれば一番簡単な解になる。
光が往復して2回変換されたことを関数の2乗で表記する表記法もあるが、それを計算するときは関数×逆関数と解釈して1に戻するのが正しい。しかし、現代の理論物理学ではそうはしない。関数を係数と解釈して係数を2乗した後で元の係数に戻すために平方根をとる。
光の往復と同じく関数を2回実行。(これは誤り)
S2(c2-v2)=c2
両辺を(c2-v2)で割り、 S2=c2/(c2-v2)
2乗されたτを元に戻すため平方根からSを求める。(これは誤り)
S=c/√(c2-v2)
右辺をcで約分する。 S=1/√(1-v2/c2)
ガリレイ変換の符号の取り違えと関数の係数化という初歩的な誤謬だけでローレンツ変換が導出できた。同様の誤謬はアインシュタインの論文をはじめ著名な解説書で確認できる。理論物理学の崩壊前にそれらを自力で探し出すのは貴重な経験になるに違いない。
観測者の立場で時間の進み方や長さが変わってしまう相対性理論では、
測定する立場の違いで時間や長さの基本単位が無限に存在している。
同じ立場で測った時間や長さどうしでなければ直接計算できないため、
相対性理論の構築段階では、数学で使う添字で厳密に書き分ける必要がある。
1秒0≠1秒v、1m0≠1mv、c0≠cv
光速度不変の光速度cは、距離と時間の比率が値cになるというだけで、
添字を付けずに距離Lや時間tを取り出して計算するのは誤り。
c0=L0/t0 ≠ cv=Lv/tv
アインシュタインも相対論学者も基本的な数学の習慣が身についていない。
初期設定からこのを添字を使っていれば、変換も展開もできずに
相対性理論やローレンツ変換は発生しない。
参考、間違いだらけのアインシュタインの論文
「運動している物体の電気力学について」について・・・ということで、マックスウェルが相対論の検証をご案内します。
 1.トリック紹介
1.トリック紹介
相対論を正しく理解するには最低限、関数のトリックとローレンツ変換の本質を知っておく必要があるよ。どのような誤りでどのようなトリックが発生するんだろう。当然、その仕組みと性質は相対論と完全に一致。
 1.トリックについて
1.トリックについて
 2.関数と理論トリック
2.関数と理論トリック
 3.ローレンツ変換をなくそう
3.ローレンツ変換をなくそう
 2.相対性理論とは
2.相対性理論とは
「相対性理論」ってなんだろう? アインシュタインがどのような問題を解決しようとしてどのような方法を使ったのかを詳しく調べると、その手法自体がトリックを生成してしまうということがわかるよ。この点を把握してからもう一度、最高の物理学理論を評価してみよう。
 1.「相対性理論」とは
1.「相対性理論」とは
 2.光速度不変の原理について
2.光速度不変の原理について
 3.相対性原理について
3.相対性原理について
 4.実証事例について
4.実証事例について
 5.相対論的効果について
5.相対論的効果について
 6.その他・注意点など
6.その他・注意点など
|
|
 3.疑似科学書解説
3.疑似科学書解説
関数のトリックを理解できない人々のうち、相対論の魅力に取り付かれた専門家が誤った解説書をどんどん出版してる。多くが物理学の啓蒙書。ところが中には論敵をバッシングするように勧める疑似科学書もある。学生たちにも悪影響を与えているので、はっきりと間違いを指摘しておくよ。
|
|
 4.検証実験などの再検証
4.検証実験などの再検証
検証実験が相対論を証明しているということは、検証式の見落としがローレンツ変換の逆変換を形成しているということ。ローレンツ変換の修正で元に戻ることが証明されているだけ。じゃあ、はじめから修正された検証式を使えば相対論はいらないネ。これからも続けられる検証実験が無駄にならないように、修正する可能性のあるポイントをあげてみたよ。
 1.マイケルソン・モーレーの実験の再検証
1.マイケルソン・モーレーの実験の再検証
相対論の立証実験とされているマイケルソン・モーレーの実験は検証式の作成から見直す必要あり。
 2.E=Mc2は架空の式
2.E=Mc2は架空の式
だれでも知っている有名な式も相対論と同じトリックによる創作なんだ。単なる仮定が世界を驚嘆させるような式に変化した原因を解説するよ。
 3.古典物理学を再考する
3.古典物理学を再考する
だいたい古典物理学は修正する必要があったのかな? 昔の人々の方がよっぽど科学的な思考で自然を理解していたと思うんだけど・・・。
 5.雑記帳
5.雑記帳
相対論以外の数学や物理など思いついたこと
 1.科学再生化計画
1.科学再生化計画
 2.数学関係
2.数学関係
 3.その他
3.その他
 6.おすすめ関連サイトリンク
6.おすすめ関連サイトリンク
相対論の誤りに気づいているサイト等を紹介
21世紀物理学の新しい公理の提案
杉岡幹生氏のHP。相対論をさまざまな角度から検証し、数学に関する学術的研究成果発表や常温核融合の話題も掲載されている。
現代科学へのいちゃもん
七色仮面さんのHP、「中途半端なお部屋」の1コーナー。海外の相対論関係の情報を中途半端とは言えないほど多数紹介されている。
![]()
Copyright© Mamoru Hidaka


